Ôn tập và kiểm tra cuối chương V

Câu 1 (1đ):

Trong không gian $Oxyz$ , cho mặt phẳng $(\alpha): \, 2x+7y-z-1=0$ . Mặt phẳng nào dưới đây song song với mặt phẳng $(\alpha)$ ?

2x-7y-z+1=0

.

x+y+9z-2=0

.

2x+7y-z+10=0

.

2x+7y+z+1=0

.

Câu 2 (1đ):

Trong không gian ${Oxyz}$ , vectơ $\overrightarrow{n}=\left(1;-1;-3 \right)$ là một vectơ pháp tuyến của mặt phẳng nào sau đây?

x-3z-3=0

.

x-y+3z-3=0

.

x+y-3z-3=0

.

x-y-3z-3=0

.

Câu 3 (1đ):

Trong không gian $Oxyz$ , cho $d$ vuông góc với $2$ đường thẳng $d_1:\,\left\{ \begin{aligned}& x=2-3t \\& y=3+t \\& z=-1+2t \end{aligned} \right.$ và ${d_2}\,:\,\dfrac{x+1}{2}=\dfrac{y}{5}=\dfrac{z+3}{3}$ . Vectơ chỉ phương của đường thẳng $d$ là

(-7;\,-13;\,17)

.

(-2;\,1;\,7)

.

(-2;\,1;\,-5)

.

(-7;\,13;\,-17)

.

Câu 4 (1đ):

Trong không gian $Oxyz$ , cho $4$ điểm $A(-1;0;2 )$ , $B(1;3;-1 )$ , $C(1;4;2 )$ , $D(0;-1;1 )$ . Sin của góc giữa đường thẳng $AD$ và mặt phẳng $(ABC )$ bằng

\dfrac{2\sqrt{138}}{69}

.

\dfrac{\sqrt{138}}{69}

.

\dfrac{4\sqrt{138}}{69}

.

\dfrac{3\sqrt{138}}{69}

.

Câu 5 (1đ):

Phương trình nào sau đây là phương trình mặt cầu?

A

x^2+2 y^2+z^2-2 x+4 y+2 z-1=0.

B

x^2+y^2+z^2-2 x-2 y+3=0.

C

2 x^2+2 y^2+2 z^2-4 x-8 y=0.

D

x^2+y^2-z^2-x-y-5=0.

Câu 6 (1đ):

Trong không gian $Oxyz$ , cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+2x-2z-7=0$ . Bán kính của mặt cầu đã cho là

9

.

3

.

\sqrt{7}

.

\sqrt{15}

.

Câu 7 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho ba điểm $A(1;-2;1)$ , $B(-1;3;3)$ , $C(2;-4;2)$ . Một vectơ pháp tuyến $\overrightarrow{n}$ của mặt phẳng $(ABC)$ là

\overrightarrow{n}=(9;4;-1)

.

\overrightarrow{n}=(9;4;1)

.

\overrightarrow{n}=(4;9;-1)

.

\overrightarrow{n}=(-1;9;4)

.

Câu 8 (1đ):

Trong không gian với hệ toạ độ $Oxyz$ , cho hai đường thẳng ${{d}_{1}},\,{{d}_{2}}$ lần lượt có phương trình ${{d}_{1}}:\dfrac{x-2}{2}=\dfrac{y-2}{1}=\dfrac{z-3}{3}$ , ${{d}_{2}}:\dfrac{x-1}{2}=\dfrac{y-2}{-1}=\dfrac{z-1}{4}$ . Phương trình mặt phẳng $\left(\alpha \right)$ cách đều hai đường thẳng ${{d}_{1}},\,{{d}_{2}}$ là

2x+y+3z+3=0

.

7x-2y-4z+3=0

.

7x-2y-4z=0

.

14x-4y-8z+3=0

.

Câu 9 (1đ):

Trong không gian $Oxyz$ , cho đường thẳng $d:\dfrac{x-1}{1}=\dfrac{y}{-1}=\dfrac{z-2}{1}$ và mặt phẳng $\left(P \right):2x-y-2z+1=0$ . Đường thẳng nằm trong $\left(P \right)$ , cắt và vuông góc với $d$ có phương trình

\dfrac{x-1}{3}=\dfrac{y+1}{4}=\dfrac{z-1}{1}

.

\dfrac{x-2}{3}=\dfrac{y+1}{4}=\dfrac{z-3}{-1}

.

\dfrac{x-2}{3}=\dfrac{y+1}{4}=\dfrac{z-3}{1}

.

\dfrac{x+2}{3}=\dfrac{y-1}{4}=\dfrac{z+3}{1}

.

Câu 10 (1đ):

Trong không gian $Oxyz$ , cho điểm $A(\dfrac{8}{3};0;0 )$ , $B(0;2;0 )$ , $C(0;0;\dfrac{8}{5} )$ và $\Delta:\left\{ \begin{aligned}& x=2-3t \\& y=-1-4t \\& z=5-5t \end{aligned} \right.$ . Khi đó góc giữa đường thẳng $\Delta$ và mặt phẳng $(ABC )$ bằng

60^\circ

.

90^\circ

.

45^\circ

.

30^\circ

.

Câu 11 (1đ):

Cho hai điểm $A(0;1;-1)$ và $B(-4;1;-5)$ . Phương trình mặt cầu nhận $AB$ làm đường kính là

x^2 + y^2 + z^2+4x-2y+6z+6=0

x^2 + y^2 + z^2-4x-2y-6z+8=0

x^2 + y^2 + z^2-4x+2y+6z+6=0

x^2 + y^2 + z^2+4x+2y-6z+8=0

Câu 12 (1đ):

Trong không gian

Oxyz,

cho phương trình mặt cầu

\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6x-2=0.

Đường kính của mặt cầu

\left( S \right)

là

2\sqrt{14}.

\sqrt{14}.

4.

8.

Câu 13 (1đ):

Trong không gian $Oxyz$ , cho điểm $I(2;6;-3 )$ và các mặt phẳng $(\alpha): \, x-2=0$ , $(\beta): \, y-6=0$ , $(\gamma): \, z+3=0$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $(\alpha)$ // $(\beta)$ .
b) $(\gamma)$ // $Oz$ .
c) $(\alpha)$ đi qua $I$ .
d) $(\beta)\bot (xOz)$ .

Câu 14 (1đ):

Trong hệ trục tọa độ cho các điểm $M(0;\,2;\,0 ),\,N(0;\,0;\,-1 ),\,P(-1;\,0;\,3 )$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Trọng tâm tam giác $MNP$ là điểm $G(0;2;1)$ .
b) Điểm $M$ thuộc mặt phẳng $(\alpha): 2x+y-2z=0$ .
c) Diện tích tam giác $OMN=1$ .
d) Tồn tại $2$ mặt phẳng $(\alpha)$ qua hai điểm $M,\ N$ và có khoảng cách từ $P$ đến $(\alpha)$ bằng $2$ .

Câu 15 (1đ):

Trong không gian $Oxyz$ , cho đường thẳng $(\Delta ):\left\{ \begin{aligned}& x=1+t \\& y=2-mt \\& z=-1+(m+1 )t \end{aligned} \right.$ và mặt phẳng $(P ):2x+y+2z-2=0$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Với $m=-4$ thì $\Delta // (P)$
b) Có vô số giá trị $m$ để $\Delta \bot (P)$
c) Với $m=-1$ thì $\Delta$ tạo với $(P)$ góc bằng $45^\circ$
d) Có hai giá trị $m$ để $\Delta$ tạo với $(P)$ góc bằng $45^\circ$ , tích hai giá trị này bằng $\dfrac{a}{b}$ ( $\dfrac{a}{b}$ là phân số tối giản, $b>0$ ). Tổng $a+b=1$ .

Câu 16 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ (đơn vị trên mỗi trục là kilômét), một trạm thu phát sóng điện thoại di động được đặt ở vị trí $I(-1; 2; 5)$ . Biết trạm thu phát sóng đó được thiết kế với bán kính phủ sóng là $4$ km.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Phương trình mặt cầu thể hiện phạm vi phủ sóng tối đa của trạm thu phát sóng là $x^2+y^2+z^2+2x-4y-10z-14=0$ .
b) Điểm $A(-1;2;8)$ nằm ngoài vùng phủ sóng của trạm thu phát sóng điện thoại di động.
c) Một người đứng ở vị trí có tọa độ điểm $B(2;0;-5)$ sẽ không thu được sóng điện thoại ở trạm phát sóng này.
d) Nếu hai người cùng bắt được sóng của trạm thu phát sóng điện thoại đó thì khoảng cách tối đa giữa hai người đó là $8$ km.

Câu 17 (1đ):

Trong không gian $Oxyz$ , cho ba điểm $A(2;0;0 ),\,B(0;1;0 ),\,C(0;0;-3 )$ . Gọi $H$ là trực tâm tam giác $ABC$ . Độ dài $OH$ có dạng $\dfrac{a}{b}$ (là phân số tối giản có mẫu dương). Tính $T=a+b$ .

Trả lời:

Câu 18 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng $d: \, \left\{\begin{aligned}& x=1+t \\& y=-t \\& z=1+2t \\ \end{aligned} \right.$ và hai mặt phẳng $(\alpha ): \, x+y-z-8=0$ , $(\beta ): \, x+y-z+2=0$ . Gọi $\Delta _1\subset (\alpha )$ , $\Delta_2\subset (\beta )$ là hai đường thẳng cùng vuông góc với $d$ lần lượt tại $A$ và $B$ . Khoảng cách từ gốc tọa độ $O$ đến mặt phẳng $(P )$ chứa $\Delta_1$ và $\Delta_2$ bằng bao nhiêu? (làm tròn kết quả đến chữ số thập phân thứ hai)

Trả lời:

Câu 19 (1đ):

Khi gắn hệ tọa độ $Oxyz$ (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng $(Oxy )$ trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí $A(1;\,-2;\,3 )$ đến vị trí $B(2;\,8;\,7 )$ . Góc giữa đường bay (một phần của đường thẳng $AB$ và sân bay (một phần của mặt phẳng $(Oxy )$ ) bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

Trả lời: .

Câu 20 (1đ):

Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ÔTÔ của bác An.

Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ÔTÔ

Đoạn đường đầu tiên có chiều rộng bằng $x$ (m), đoạn đường thẳng vào cổng GARA có chiều rộng $2,6$ (m). Biết kích thước xe ôtô là $5$ m x $1,9$ m (chiều dài $x$ chiều rộng). Để tính toán và thiết kế đường đi cho ôtô người ta coi ôtô như một khối hộp chữ nhật có kích thước chiều dài là $5$ (m), chiều rộng $1,9$ (m). Tìm chiều rộng nhỏ nhất của đoạn đường đầu tiên để ôtô có thể đi vào GARA được? (Làm tròn kết quả đến hàng phần mười của méti; giả thiết ôtô không đi ra ngài đường, không đi nghiêng và ôtô không bị biến dạng).

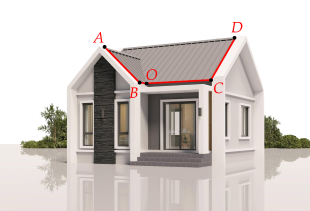
Trả lời:

Câu 21 (1đ):

Trong không gian với hệ trục tọa độ $Oxyz$ , cho mặt cầu $(S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=1$ và mặt phẳng $(P):x+y+z-1=0$ . Gọi $(S')$ là mặt cầu chứa đường tròn giao tuyến của $(S)$ và $(P)$ đồng thời tiếp xúc với mặt phẳng $(Q):x+1=0$ . Gọi $I(a;b;c)$ là tâm của mặt cầu $\left( {S'} \right)$ , tính giá trị $T=a+b+c$ .

Trả lời: .

Câu 22 (1đ):

Một robot khảo sát không gian hoạt động trong môi trường $3D$ có một cảm biến hình cầu, được lập trình để di chuyển sao cho cảm biến này tiếp xúc tại một điểm $Q$ trên một bức tường nghiêng có phương trình là mặt phẳng $x+y-z-3=0$ để đo đạc. Trong lúc khảo sát, cảm biến luôn phải đi qua hai điểm chuẩn đã cố định sẵn trong không gian là điểm $M(1;1;1)$ - vị trí cảm biến tại lần đo đầu tiên và điểm $N(-3;-3;-3)$ - vị trí cảm biến tại lần đo tiếp theo. Để tối ưu hoá phần mềm điều hướng, kỹ sư muốn xác định rằng: Dù cảm biến (hình cầu) có di chuyển sao cho tiếp xúc ở đâu trên bức tường, điểm tiếp xúc đó luôn nằm trên một đường tròn cố định.

Tính bán kính của đường tròn cố định đó, từ đó giúp lập trình robot dò tìm tiếp điểm dễ dàng hơn trong các lần đo tiếp theo.

Trả lời:

Bài học cùng chủ đề

Ôn tập và kiểm tra cuối chương V SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Ôn tập và kiểm tra cuối chương V SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP