Bài học cùng chủ đề
- Tam giác đều. Hình vuông. Lục giác đều
- Tam giác đều
- Hình vuông
- Chu vi và diện tích hình vuông
- Hình lục giác đều
- Nhận diện hình vuông, tam giác đều, lục giác đều
- Vẽ hình vuông, tam giác đều, lục giác đều
- Một số yếu tố của hình tam giác đều, hình vuông và hình lục giác đều
- Chu vi, diện tích hình vuông
- Phiếu bài tập: Hình vuông. Hình tam giác đều. Hình lục giác đều
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nhận diện hình vuông, tam giác đều, lục giác đều SVIP
Đây là bản xem thử, hãy nhấn Luyện tập ngay để bắt đầu luyện tập với OLM
Câu 1 (1đ):



Chọn hình ảnh xuất hiện tam giác đều.



Câu 2 (1đ):




Chọn những hình ảnh xuất hiện hình vuông.




Câu 3 (1đ):




Chọn những hình ảnh xuất hiện hình lục giác đều.




Câu 4 (1đ):



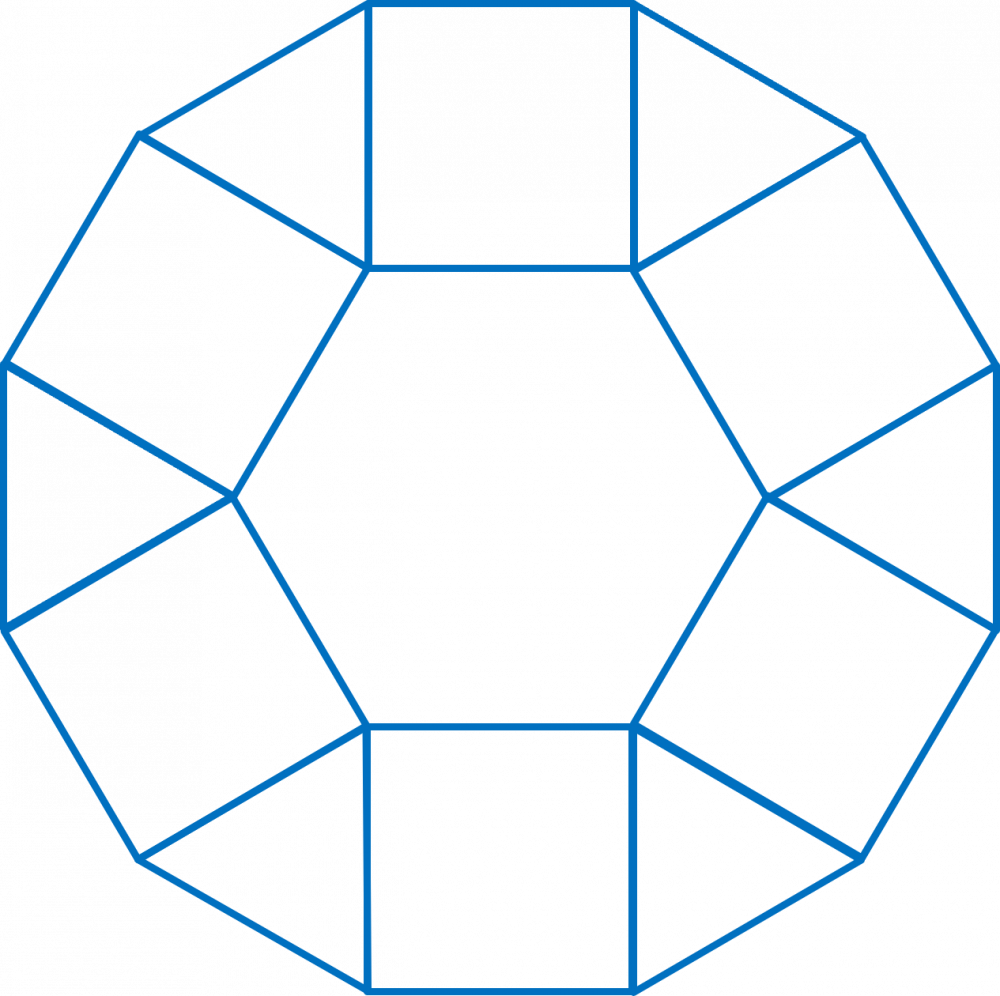
Mẫu họa tiết nào dưới đây có cả hình vuông, tam giác đều và hình lục giác đều?




Câu 5 (1đ):
Những tam giác nào sau đây không phải tam giác đều?
Tam giác DHC.
Tam giác ADH.
Tam giác AHC.
Tam giác ABC.
Câu 6 (1đ):
Cho tam giác đều ABC và các điểm E; D; F như hình vẽ. Những khẳng định nào sau đây đúng?
Góc ADF bằng 60∘.
AD = AB.
Góc ABC bằng góc ACB.
AE = ED.
Câu 7 (1đ):
Có tất cả bao nhiêu tam giác đều trong hình vẽ?
3.
6.
5.
4.
Câu 8 (1đ):
Các hình vuông có trong hình vẽ trên là
HBCF.
HGFE.
ABCD.
Câu 9 (1đ):
là hai cạnh; BD là
.
Quan sát hình trên và hoàn thành câu sau.
Trong hình vuông ABCD, AB và A
- C
- D
- O
- đỉnh
- đường chéo
- cạnh
Câu 10 (1đ):
Hình vẽ sau có tất cả bao nhiêu hình vuông?
1.
2.
4.
3.
Câu 11 (1đ):
;
;
.
Hoàn thành các kết luận sau.
Trong hình lục giác đều ABCDEG có:
AD là
- đường chéo phụ
- đường chéo chính
DG là
- đường chéo phụ
- đường chéo chính
BC là
- cạnh
- đỉnh
Câu 12 (1đ):
Có tất cả hình lục giác đều trong hình vẽ trên.
25%
Đúng rồi !

Hôm nay, bạn còn lượt làm bài tập miễn phí.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
