Làm quen với xác suất của biến cố. SVIP

1. Xác suất của biến cố

Khả năng xảy ra của một biến cố được đo lường bởi một số nhận giá trị từ 0 đến 1, gọi là xác suất của biến cố đó. 

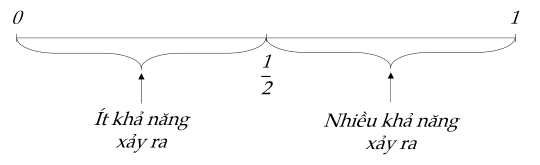
Nhận xét: Xác suất của một biến cố càng gần 1 thì biến cố đó càng nhiều khả năng xảy ra. Xác suất của một biến cố càng gần 0 thì biến cố đó càng ít khả năng xảy ra. 

Ví dụ 1:

- Người ta tính được xác suất để trúng được giải độc đắc của xổ số Vietlott 6/45 (Một loại xổ số đang được lưu hành ở Việt Nam) là $0,0000001228$ hay $0,00001228\%$.

- Bản tin dự báo thời tiết ghi: Khả năng (hay xác suất) có mưa là $43\%$.

- Xác suất để xuất hiện mặt sấp khi gieo một đồng xu cân đối là $\displaystyle\frac{1}{2}$ hay $50\%$.

Ví dụ 2: Các chuyên gia bóng đá nhận định trong trận bóng đá ngày mai giữa đội A và đội B, xác suất thắng của đội A là $60\%$, xác suất thua là $35\%$ và xác suất hoà là $5\%$. Theo nhận định trên, đội nào có xác suất thắng cao hơn?

Giải

Xác suất thua của đội A là $35\%$, hay xác suất thắng của đội B là $35\%$. Xác suất thắng của đội A cao hơn đội B. Vậy đội A có khả năng thắng cao hơn.

2. Xác suất của một biến cố đơn giản 

a. Xác suất của biến cố chắc chắn, biến cố không thể

Khả năng xảy ra của biến cố chắc chắn là $100\%$. Vậy biến cố chắc chắn có xác suất bằng $1$.

Khả năng xảy ra của biến cố không thể là $0\%$. Vậy biến cố không thể có xác suất bằng $0$.

Ví dụ 3: 

- Xác suất của biến cố A: "Ngày mai, mặt trời mọc ở phía Tây" bằng $0$ vì A là biến cố không thể.

- Xác suất của biến cố B: "Tháng 3 có ít hơn 32 ngày" bằng $1$ vì B là biến cố chắc chắn.

b. Xác suất của các biến cố đồng khả năng

Gieo một đồng xu cân đối. Xét hai biến cố sau:

A: "Đồng xu xuất hiện mặt ngửa".

B: "Đồng xu xuất hiện mặt sấp".

Do đồng xu cân đối nên biến cố A và biến cố B có khả năng xảy ra như nhau. Ta nói hai biến cố A và B là đồng khả năng.

Vì chỉ xảy ra biến cố A hoặc biến cố B nên xác suất của biến cố A và xác suất của biến cố B bằng nhau và bằng $\displaystyle \frac{1}{2}$ (hay $50\%$).

Nhận xét: Nếu chỉ xảy ra hoặc A hoặc B và hai biến cố A, B là đồng khả năng thì xác suất của chúng bằng nhau và bằng $0,5$.

Ví dụ 4: Trong buổi liên hoan, lớp 7A tổ chức trò chơi Rút phiếu trúng thưởng. Cô giáo đã chuẩn bị 10 lá phiếu giống nhau ghi các số từ 1 đến 10, được gấp lại và đặt trong hộp. Mỗi bạn lần lượt rút  ngẫu nhiên một lá phiếu và sẽ trúng thưởng nếu rút được phiếu ghi số 5. Bạn Mai rút được phiếu đầu tiên. Tính xác suất để Mai rút được phiếu trúng thưởng.

Giải

Xét 10 biến cố sau:

$E_1$: "Rút được lá phiếu ghi số 1";

$E_2$: "Rút được lá phiếu ghi số 2";

$E_3$: "Rút được lá phiếu ghi số 3";

$E_4$: "Rút được lá phiếu ghi số 4";

$E_5$: "Rút được lá phiếu ghi số 5";

$E_6$: "Rút được lá phiếu ghi số 6";

$E_7$: "Rút được lá phiếu ghi số 7";

$E_8$: "Rút được lá phiếu ghi số 8";

$E_9$: "Rút được lá phiếu ghi số 9";

$E_{10}$: "Rút được lá phiếu ghi số 10".

Vì Mai rút phiếu ngẫu nhiên nên khả năng xảy ra của mỗi biến cố $E_1$, $E_2$, ..., $E_{10}$ là như nhau. Ta nói 10 biến cố này đồng khả năng. Mặt khác, trong mỗi lần rút phiếu luôn xảy ra duy nhất một trong các biến cố này nên xác suất của cúng bằng nhau và bằng $\displaystyle \frac{1}{10}$. Vậy xác suất để Mai rút được lá phiếu trúng thưởng là $\displaystyle \frac{1}{10}$.

Trong một trò chơi hay thí nghiệm, nếu có $k$ biến cố đồng khả năng và luôn xảy ra duy nhất một trong $k$ biến cố này thì xác suất của mỗi biến cố đó đều bằng $\displaystyle\frac{1}{k}$.