Từ trường của dòng điện chạy trong các dây dẫn có hình dạng đặc biệt SVIP

I. Từ trường của dòng diện chạy trong dây dẫn thẳng dài

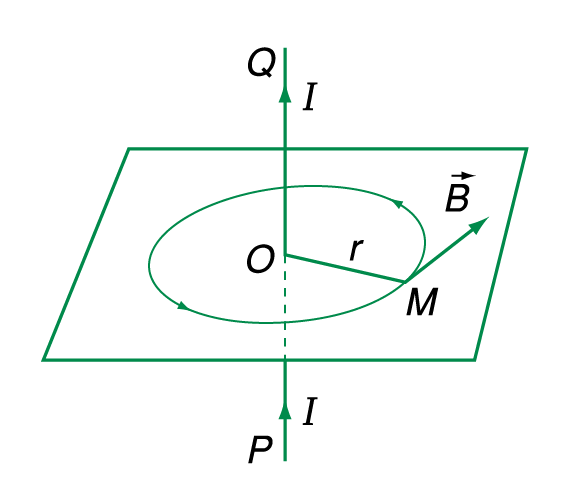
• Cảm ứng từ \(\overrightarrow{B}\) vuông góc với mặt phẳng tạo bởi M và dây dẫn.
• \(\overrightarrow{B}\) có chiều được xác định theo quy tắc nắm bàn tay phải
• Độ lớn cảm ứng từ tại điểm cách dây dẫn một khoảng \(OM=r\) là

\(B=2.10^{-7}\dfrac{I}{r}\)

II. Từ trường của dòng điện chạy trong dây dẫn uốn thành vòng tròn

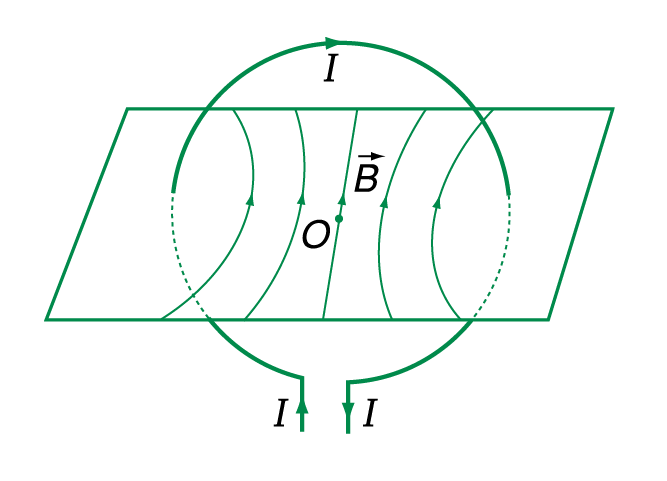
Các đường sức từ của dòng điện tròn là là những đường cong có chiều đi vào mặt Nam, đi ra mặt Bắc của dòng điện tròn ấy. Đường sức đi qua tâm O là đường thẳng vô hạn ở hai đầu.

• Cảm ứng từ \(\overrightarrow{B}\) tại tâm O có phương vuông góc với mặt phẳng dòng điện
• \(\overrightarrow{B}\) có chiều đi vào mặt Nam, đi ra mặt Bắc
• Độ lớn cảm ứng từ tại tâm O của vòng dây có bán kính \(R\) là

​\(B=2\pi.10^{-7}\dfrac{I}{R}\)

Nếu ống dây có \(N\)  vòng khít nhau thì

\(B=2\pi.10^{-7}N\dfrac{I}{R}\)

III. Từ trường của dòng điện chạy trong ống dây dẫn hình trụ

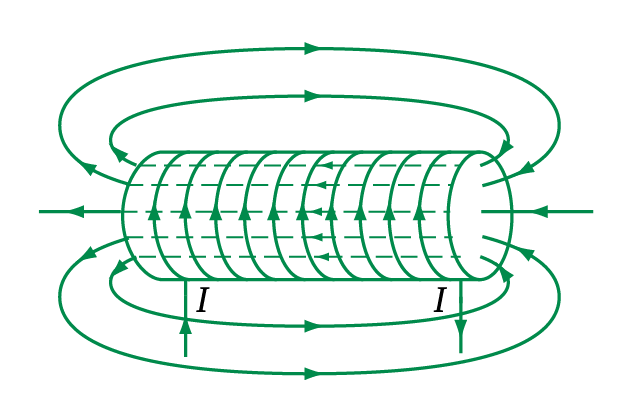
• Trong ống dây các đường sức từ là những đường thẳng song song cùng chiều và cách đều nhau
• Cảm ứng từ trong lòng ống dây:

​\(B=4\pi.10^{-7}\dfrac{N}{l}I=4\pi.10^{-7}nI\)

Trong đó: \(N\) là số vòng dây; \(l\) là độ dài hình trụ; \(n\) là số vòng dây trên một đơn vị dài

IV. Từ trường của nhiều dòng điện

Vectơ cảm ứng từ tại một điểm do nhiều dòng điện gây ra bằng tổng các véc tơ cảm ứng từ do từng dòng điện gây ra tại điểm ấy

\(\overrightarrow{B}=\overrightarrow{B_1}+\overrightarrow{B_2}+...+\overrightarrow{B_n}\)

• Khi \((\overrightarrow{B_1},\overrightarrow{B_2})=\alpha\) thì: \(B^2=B_1^2+B_2^2+2B_1B_2\cos\alpha\)
• Khi \(\overrightarrow{B_1}\nearrow\nearrow\overrightarrow{B_2}\) thì: \(B=B_1+B_2\)
• Khi \(\overrightarrow{B_1}\nearrow\swarrow\overrightarrow{B_2}\) thì: \(B=\left|B_1-B_2\right|\)
• Khi \(\overrightarrow{B_1}\bot\overrightarrow{B_2}\) thì: \(B=\sqrt{B_1^2+B_2^2}\)