Khái niệm vectơ SVIP

I. KHÁI NIỆM VECTƠ

Vectơ là một đoạn thẳng có hướng.

Chú ý. 

• Vectơ có điểm đầu là \(A\) và điểm cuối \(B\) được kí hiệu là \(\overrightarrow{AB}\) đọc là vectơ \(AB\).

•  Để vẽ một vectơ, ta vẽ một đoạn thẳng nối điểm đầu và điểm cuối của nó, rồi đánh dấu mũi tên ở điểm cuối.
• Đối với vectơ \(\overrightarrow{AB}\) ta gọi:

- Đường thẳng đi qua hai điểm \(A\) và \(B\) là giá của vectơ \(\overrightarrow{AB}\).

- Độ dài đoạn thẳng \(AB\) là độ dài của vectơ \(\overrightarrow{AB}\), kí hiệu là \(\left|\overrightarrow{AB}\right|\).

II. VECTƠ CÙNG PHƯƠNG, VECTƠ CÙNG HƯỚNG

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Nhận xét: Nếu hai vectơ cùng phương thì hoặc chúng cùng hướng hoặc chúng ngược hướng.

Ví dụ: Trong hình vẽ sau

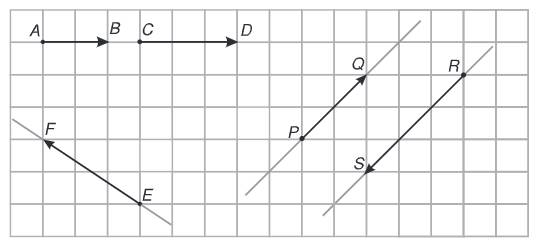
Ta có:

• Vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) có giá trùng nhau. Vectơ \(\overrightarrow{PQ}\) và \(\overrightarrow{RS}\) có giá song song với nhau.
• Có hai cặp vectơ cùng phương với nhau là:  \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) ; \(\overrightarrow{PQ}\) và \(\overrightarrow{RS}\).
• Vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) là hai vectơ cùng hướng. Vectơ \(\overrightarrow{PQ}\) và \(\overrightarrow{RS}\) là hai vectơ ngược hướng.

III. HAI VECTƠ BẰNG NHAU

Hai vectơ \(\overrightarrow{AB},\overrightarrow{CD}\) bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: \(\overrightarrow{AB}=\overrightarrow{CD}.\)

Chú ý. Vectơ còn được kí hiệu là \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},...\)

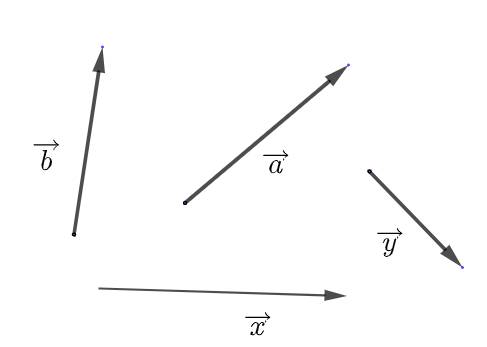
• Độ dài của vectơ \(\overrightarrow{AB},\overrightarrow{a}\) tương ứng được kí hiệu là \(\left|\overrightarrow{AB}\right|,\left|\overrightarrow{a}\right|\).

Nhận xét:

• Hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu \(\overrightarrow{a}=\overrightarrow{b}.\)
• Khi cho trước vectơ \(\overrightarrow{a}\) và điểm \(O\), ta luôn tìm được một điểm \(A\) duy nhất sao cho \(\overrightarrow{OA}=\overrightarrow{a}.\) 

IV. VECTƠ-KHÔNG

Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là \(\overrightarrow{0}.\)

Nhận xét: Hai điểm \(A,B\) trùng nhau khi và chỉ khi \(\overrightarrow{AB}=\overrightarrow{0}.\)

V. BIỂU THỊ MỘT SỐ ĐẠI LƯỢNG CÓ HƯỚNG BẰNG VECTƠ

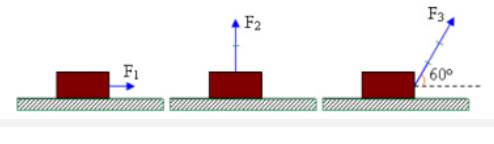
Trong vật lí, một số đại lượng như: lực, vận tốc,...là đại lượng có hướng. Người ta dùng vectơ để biểu thị các đại lượng có hướng đó. Hướng của vectơ chỉ hướng của đại lượng, độ dài vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.