Bài tập tự luận (Nâng cao) SVIP

Hướng dẫn giải:

Ta có: $\overrightarrow{A B}=\overrightarrow{D C} ; \overrightarrow{B A}=\overrightarrow{C D} ; \overrightarrow{A D}=\overrightarrow{B C} ; \overrightarrow{D A}=\overrightarrow{C B} ; \overrightarrow{A O}=\overrightarrow{O C} ; \overrightarrow{O A}=\overrightarrow{C O} ; \overrightarrow{O B}=\overrightarrow{D O} ; \overrightarrow{B O}=\overrightarrow{O D}$.

Hướng dẫn giải:

Theo giả thiết, ta có: $D, E, F$ lần lượt là trung điểm của $B C, C A, A B$.

$\Rightarrow E F$ là đường trung bình $\triangle A B C$ và $E F=\dfrac{1}{2} B C$ (1).
Lại có $D$ là trung điểm $B C \Rightarrow C D=\dfrac{1}{2} C B(2)$.

Dễ thấy $\overrightarrow{E F}$ cùng hướng $\overrightarrow{C D}(3)$

Từ (1), (2), (3) $\Rightarrow \overrightarrow{E F}=\overrightarrow{C D}$.

Hướng dẫn giải:

- Chứng minh $\overrightarrow{A M}=\overrightarrow{N C}$.

Ta có:
$M$ trung điểm $B C \rightarrow M C=\dfrac{1}{2} B C$.

$N$ trung điểm $A D \rightarrow A N=\dfrac{1}{2} A D$.

Mà $A D=B C \Rightarrow A N=M C \Rightarrow$ Tứ giác $A M C N$ là hình bình hành $\Rightarrow \overrightarrow{A M}=\overrightarrow{N C}$.

- Chứng minh $\overrightarrow{D K}=\overrightarrow{N I}$.

$ \begin{aligned} &\text { Ta có: }\left\{\begin{array}{l} A N / / M B \\ A N=M B \Rightarrow A B M N \text { là hình bình hành } \Rightarrow I \text { là trung điểm } N B \Rightarrow N I=\dfrac{1}{2} N B(1) . \\ M N / / A B \end{array}\right. \\ &\text { Ta có: }\left\{\begin{array}{l} D N / / M C \\ D N=M C \Rightarrow C D N M \text { là hình bình hành } \Rightarrow K \text { là trung điểm } M D \Rightarrow D K=\dfrac{1}{2} D M(2) \text {. } \\ M N / / D C \end{array}\right. \end{aligned} $

Dễ thấy $B N D M$ là hình bình hành do $\left\{\begin{array}{l}B N / / M D \\ B N=M D\end{array}\right.$ nên $N D=B M(3)$.

Từ (1),(2),(3) $\Rightarrow \overrightarrow{D K}=\overrightarrow{N I}$.

Hướng dẫn giải:

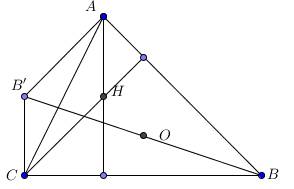
Ta có $B^{\prime}$ là điểm đối xứng của $B$ qua $O$ nên $B B^{\prime}$ là một đường kính của đường tròn ngoại tiếp tam giác $A B C$.

Ta có: $O C=\dfrac{1}{2} B B^{\prime}$ nên tam giác $C B B^{\prime}$ vuông tại $C$.

Ta có: $\left\{\begin{array}{l}B^{\prime} C \perp B C \\ A H \perp B C\end{array} \Rightarrow B^{\prime} C / / A H\right.$

Tương tự: $O A=\dfrac{1}{2} B B^{\prime}$ nên tam giác $A B B^{\prime}$ vuông tại $A$.

Ta có: $\left\{\begin{array}{l}B^{\prime} A \perp A B \\ C H \perp A B\end{array} \Rightarrow B^{\prime} A / / CH\right.$

Từ (1) và (2) ta có tứ giác $A H C B^{\prime}$ là hình bình hành. Suy ra $\overrightarrow{A H}=\overrightarrow{B^{\prime} C}$.

Hướng dẫn giải:

Vì $H$ là trực tâm của tam giác $A B C$
nên $H B \perp A C$
Vì tia $A O$ cất đường tròn tâm $O$ tại $D$
nên $A D$ là đường kính của đường tròn tâm $O$.
$\begin{aligned}&\Rightarrow A C D=90^{\circ} \\&\Leftrightarrow C D \perp A C\end{aligned}$
$\Rightarrow H B / / C D$
Chứng minh tương tự $\Rightarrow B D / / H C$.

Hướng dẫn giải:

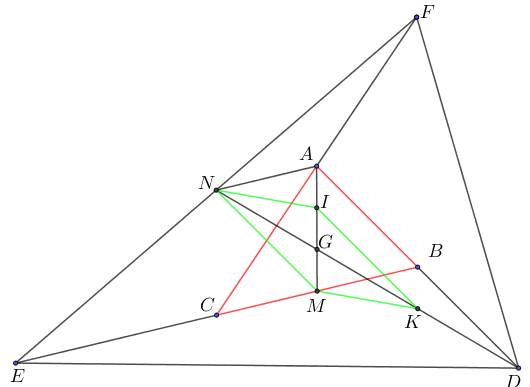
a) $\overrightarrow{A B}=\overrightarrow{N M}$.
Ta có $A, N$ lần lượt là trung điểm của $F C, F E$

$\Rightarrow \overrightarrow{A N}=\dfrac{1}{2} \overrightarrow{C E}=\dfrac{1}{2} \overrightarrow{B C} .$

Mà $\overrightarrow{B M}=\dfrac{1}{2} \overrightarrow{B C}$ suy ra $\overrightarrow{A N}=\overrightarrow{B M} \Rightarrow$ tứ giác $A N M B$ là hình bình hành $\Rightarrow \overrightarrow{N M}=\overrightarrow{A B}$.

b) $\overrightarrow{M K}=\overrightarrow{N I}$.
Ta có $I, K$ lần lượt là trung điểm của $G A$ và $G D \Rightarrow \overrightarrow{I K}=\dfrac{1}{2} \overrightarrow{A D}=\overrightarrow{A B}=\overrightarrow{N M} \Rightarrow$ tứ giác $I N M K$ là hình bình hành nên $\overrightarrow{M K}=\overrightarrow{N I}$.

Hướng dẫn giải:

Ta có $G$ là trọng tâm $\triangle A B C \Rightarrow \overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{0}$ (1).
Và $G$ là trọng tâm $\Delta A E F \Rightarrow \overrightarrow{G A}+\overrightarrow{G E}+\overrightarrow{G F}=\overrightarrow{0}(2)$.
Từ (1) và $(2)$ :
$\Rightarrow \overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{G A}+\overrightarrow{G E}+\overrightarrow{G F} \Leftrightarrow \overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{G E}+\overrightarrow{G F} \Leftrightarrow \overrightarrow{G C}-\overrightarrow{G F}=\overrightarrow{G E}-\overrightarrow{G B} \Leftrightarrow \overrightarrow{F C}=\overrightarrow{B E}$.