Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Góc nội tiếp SVIP
Trên cạnh huyền BC của tam giác vuông ABC về phía ngoài ta dựng hình vuông với tâm tại điểm O. Chứng minh rằng AO là tia phân giác của góc vuông.
Hướng dẫn giải:
Chứng minh được bốn điểm A, B, O, C cùng thuộc một đường tròn và số đo góc BAO bằng số đo góc BCO (cùng chắn cung BO).
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Từ đỉnh A ta kẻ đường cao AH (H $\in$ BC). Chứng minh rằng $\widehat{BAH}=\widehat{OAC}$.
Hướng dẫn giải:
Chú ý rằng \(\widehat{OEC}=\widehat{OBC}\) (cùng chắn cung AC).
Cho tam giác ABC nội tiếp đường tròn tâm O. Tia phân giác của góc BAC cắt BC ở D và cắt đường tròn (O) tại E. Chứng minh rằng:
a) AB . AC = AD . AE;
b) ED . EA = EB2.
Hướng dẫn giải:
Đưa về chứng minh các đẳng thức tỉ số.
\(AB.AC=AD.AE\Leftrightarrow\dfrac{AB}{AD}=\dfrac{AC}{AE};\)
\(ED.EA=EB^2\Leftrightarrow\dfrac{ED}{EB}=\dfrac{EB}{EA}.\)
Xem hướng dẫn.
Cho tam giác ABC nội tiếp đường tròn (O ; R) có AB = 8cm, AC = 15cm, đường cao AH = 5cm (điểm H nằm trên cạnh BC). Tính bán kính của đường tròn.
Hướng dẫn giải:
Kẻ đường kính AD, chứng minh được △AHB $\backsim$ △ACD.
(Định lý sin) Cho tam giác nhọn ABC có BC = a, AC = b, AB = c và nội tiếp đường tròn (O ; R). Chứng minh rằng:
$\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}=2R$.
Hướng dẫn giải:
Kẻ đường kính BD.
Ta có: BC = BD . sin D = 2R . sin A.
Cho hình vẽ, biết rằng CA // DE. Tính số đo $\widehat{ODE}$ và $\widehat{OAB}$.
Hướng dẫn giải:
Cho hai đường tròn (O) và (O') cắt nhau ở A và B. Qua A kẻ hai đường thẳng CD và EF, cắt (O) tại C và E, cắt (O') tại D và F sao cho $\widehat{EAB}=\widehat{DAB}$. Chứng minh rằng CD = EF.
Hướng dẫn giải:
Kẻ BH $\bot$ EF, BK $\bot$ CD.
Chú ý rằng AB là tia phân giác góc EAD nên B cách đều hai cạnh AE và AD.
Quan sát hai tam giác vuông EBH và CBK có đặc điểm gì?
Chứng minh được EH = CK. Tương tự, FH = DK.
Cho nửa đường tròn $(O)$ đường kính $AB$ và dây cung AC. Gọi $M$, $N$ lần lượt là các điểm chính giữa của các cung $AC$ và $BC$. Hai dây $AN$ và $BM$ cắt nhau tại $I$. Chứng minh $CI$ là tia phân giác của góc $ACB$.
Hướng dẫn giải:

Do M là điểm chính giữa cung AC nên \(\widehat{CBM}=\widehat{MBA}\) hay BM là tia phân giác của góc CBA.
Do N là điểm chính giữa cung BC nên \(\widehat{CAN}=\widehat{NAB}\) hay AN là tia phân giác của góc CAB.
Mà BM và AN cắt nhau ở I nên I là tâm đường tròn nội tiếp tam giác ABC.
Suy ra CI là tia phân giác góc BCA.
Cho đường tròn $(O)$ đường kính $AB$ và một điểm $C$ đi động trên đường tròn đó. Vẽ đường tròn $(I)$ tiếp xúc với đường tròn $(O)$ tại $C$ và tiếp xúc với đường kính $AB$ tại $D$, đường tròn này cắt $CA$ và $CB$ lần lượt tại các điểm thứ hai là $M$ và $N$. Chứng minh rằng:
a) Ba điểm $M$, $I$, $N$ thẳng hàng.
b) \(ID\perp MN\).
c) Đường thẳng $CD$ đi qua một điểm cố định.
Hướng dẫn giải:

a) Do \(\widehat{MCN}=\widehat{ACB}=90^o\) nên MN là đường kính của đường tròn tâm (I) hay M, N, I thẳng hàng.
b) Có \(\widehat{INC}=\widehat{ICN}=\widehat{CBA}\) nên MN // AB. Mà \(ID\perp AB\Rightarrow ID\perp MN\).
c) Vì ID vuông góc với đường kính MN của đường tròn (I) nên D là trung điểm cung MN của đường tròn đó và CD là phân giác của góc ACB. Suy ra đường thẳng CD đi qua trung điểm E của cung AB của đường tròn (O).
Cho nửa đường tròn $(O)$ đường kính \(AB=2R\) và điểm $C$ nằm trong nửa mặt phẳng chứa nửa đường tròn và nằm ngoài nửa đường tròn. $CA$ cắt nửa đường tròn ở $M$, $CB$ cắt nửa đường tròn ở $N$. Gọi $H$ là giao điểm của $AN$ và $BM$.
a) Chứng minh \(CH\perp AB\).
b) Gọi $I$ là trung điểm của $CH$. Chứng minh $MI$ là tiếp tuyến của nửa đường tròn $(O)$.
c) Giả sử $CH$ = $2R$. Tính số đo cung \(\stackrel\frown{MN}\).
Hướng dẫn giải:

a) Dễ thấy H là trực tâm tam giác ABC nên \(CH\perp AB\).
b) Gọi K là giao điểm của CI và AB.
Có I là trung điểm CH nên I là tâm đường tròn ngoại tiếp tam giác vuông CMH, do đó:
\(\widehat{IMH}=\widehat{IHM}=\widehat{KHB}=\widehat{MAK}\) (Vì MAKH là tứ giác nội tiếp) \(=90^o-\widehat{OMB}\).
\(\Rightarrow\widehat{IMH}+\widehat{OMB}=90^o\Rightarrow\widehat{IMO}=90^o\) nên MI là tiếp tuyến của nửa đường tròn (O).
c) Do \(CH=2R\) nên \(\Delta MCH=\Delta MBA\) và \(\Delta CHN=\Delta ABN\).
\(\Delta MCH=\Delta MBA\) suy ra \(MC=MB\). Vì vậy \(\Delta MBC\) vuông cân.
Suy ra \(\widehat{MCB}=\widehat{CBM}=45^o\).
Suy ra \(\stackrel\frown{MN}=2\widehat{CBM}=2.45^o=90^o.\)
Trên cung nhỏ $BC$ của đường tròn ngoại tiếp tam giác đều $ABC$ lấy một điểm $P$ tùy ý. Gọi $Q$ là giao điểm của $AP$ và $BC$.
a) Chứng minh rằng \(BC^2=AP.AQ\).
b) Chứng minh \(BP+PC=AP\).
c) Chứng minh \(\dfrac{1}{PQ}=\dfrac{1}{PB}+\dfrac{1}{PC}\).
Hướng dẫn giải:
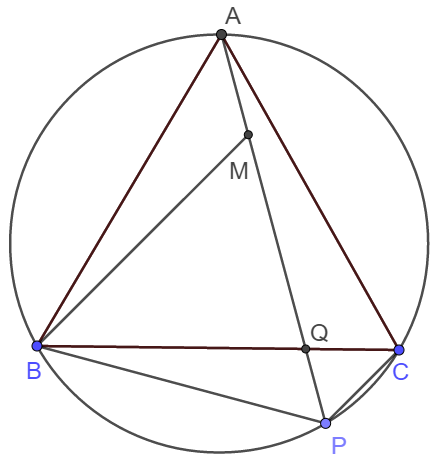
a) Tam giác ABC đều nên \(\widehat{ABC}=\widehat{BAC}=\widehat{BCA}=60^o\).
Suy ra \(\stackrel\frown{AB}=\stackrel\frown{BC}=\stackrel\frown{CA}=120^o\)
Vì vậy \(\widehat{BPA}=60^o\).
Xét tam giác BAQ và tam giác PAB có: \(\widehat{A}\) chung và \(\widehat{ABQ}=\widehat{BPA}=60^o\) suy ra \(\Delta BAQ\) đồng dạng với \(\Delta PAB\) (g-g).
Suy ra \(\dfrac{BA}{PA}=\dfrac{AQ}{AB}\) \(\Leftrightarrow AB^2=AP.AQ\).
mà \(AB=BC\) suy ra \(BC^2=AP.AQ\).
b) Trên đoạn PA lấy điểm M sao cho PM = PB thì ta có tam giác PMB là tam giác đều (Tam giác cân với một góc bằng 60o) .
Hơn nữa, vì \(\widehat{ABC}=60^o=\widehat{PBM}\Rightarrow\widehat{ABM}=\widehat{PBC}\)
Vậy nên \(\Delta ABM=\Delta CBP\left(c-g-c\right)\Rightarrow AM=PC.\)
Vì vậy \(PB+PC=PM+AM=PA\).
c) Giả sử \(\dfrac{1}{PQ}=\dfrac{1}{PB}+\dfrac{1}{PC}\)\(\Leftrightarrow\dfrac{1}{PQ}=\dfrac{PC+PB}{PB.PC}=\dfrac{AP}{PB.PC}\).
Suy ra \(PB.PC=PQ.AP\).
Xét tam giác BAP và tam giác PCB có:
\(\widehat{BAP}=\widehat{BCP}\)
\(\widehat{BPC}=\widehat{BMA}=120^o\)
Suy ra tam giác BAP đồng dạng với tam giác PCB. (1)
Xét tam giác BPC và tam giác PQC có:
\(\widehat{C}\) chung và \(\widehat{PQC}=\widehat{BPC}=120^o\).
Suy ra \(\Delta BPC\) đồng dạng với \(\Delta PQC\) (g-g)( 2)
Từ (1) và (2) suy ra \(\Delta BAP\) đồng dạng với \(\Delta PQC\).
Từ đó suy ra \(\dfrac{PB}{PQ}=\dfrac{AP}{PC}\)\(\Leftrightarrow PB.PC=PQ.AP\) (đpcm).
Cho đường tròn (O ; R), các đường kính AB và CD vuông góc với nhau. Gọi I là trung điểm của BO. Tia CI cắt đường tròn tại E, EA cắt CD ở K. Tính độ dài DK.
Hướng dẫn giải:
Chứng minh được ΔAOK $\backsim$ ΔAEB.








