Bài học cùng chủ đề
- Một số hệ thức giữa cạnh và góc trong tam giác vuông
- Hệ thức giữa cạnh huyền và cạnh góc vuông trong tam giác vuông
- Hệ thức giữa hai cạnh góc vuông trong tam giác vuông
- Giải tam giác vuông
- Phiếu bài tập tuần: Hệ thức lượng trong tam giác vuông
- Giải tam giác vuông
- Giải tam giác nhọn
- Ứng dụng hệ thức giữa cạnh và góc trong ước lượng chiều cao, khoảng cách, tính góc
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Giải tam giác nhọn SVIP
Cho tam giác $ABC$ có $\widehat{B}=65^\circ , \, \widehat{C}=45^\circ $ và $AB=2,8$ cm. Tính các góc và cạnh còn lại của tam giác đó (gọi là giải tam giác $ABC$).
Hướng dẫn giải:

Ta có $\widehat{A}=180^\circ -\widehat{B}-\widehat{C}=70^\circ $.
Kẻ đường cao $AH$.
Xét $\Delta ABH$ vuông tại $H$, ta có $AH=AB.\sin \widehat{B}=2,8.\sin 65^\circ \approx 2,54$ (cm).
Tương tự $BH=AB.\cos \widehat{B}=2,8.\cos 65^\circ \approx 1,18$ (cm).
Mặt khác do giả thiết suy ra tam giác $HAC$ vuông cân tại $H$ nên $HA=HC$.
Do đó $BC\approx 2,54+1,18=3,7$ (cm).
Xét $\Delta AHC$ vuông tại $H$, ta có $AC=\dfrac{HA}{\sin C}=\dfrac{2,54}{\sin 45^\circ }\approx 3,6$ (cm).
Giải tam giác $ABC$ có $\widehat{B}=65^\circ , \, \widehat{C}=40^\circ $ và $BC=4,2$ cm.
Hướng dẫn giải:

Ta có $\widehat{A}=180{}^\circ -\widehat{B}-\widehat{C}=75^\circ $
Kẻ đường cao $BH$.
Xét $\Delta BCH$ vuông tại $H$, ta có:
$BH=BC.\sin \widehat{C}=4,2.\sin 40^\circ \approx 2,70$ (cm)
Tương tự, xét $\Delta ABH$ vuông tại $H$, ta có:
$AB=\dfrac{BH}{\sin \widehat{A}}=\dfrac{2,70}{\sin 75^\circ }\approx 2,8$ (cm)
Mặt khác ta có $ AC=AH+CH=BH.\big( \cot \widehat{A}+\cot \widehat{C} \big) \approx 2,70.\left( \cot 75^\circ +\cot 40^\circ \right)\approx 3,9$ cm.
Giải tam giác $ABC$ có $\widehat{B}=70^\circ $ và $AB=2,1$ cm; $AC=3,8$ cm.
Hướng dẫn giải:
Vẽ $AH \bot BC$.
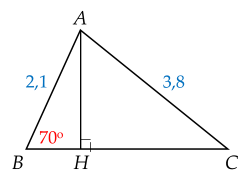
Xét $\Delta ABH$ vuông tại $H$ có $AH=AB.\sin \widehat{B}=2,1.\sin 70^\circ \approx 1,97$
Tương tự, xét $BH=AB.\cos \widehat{B}=2,1.\cos 70^\circ \approx 0,72$
Mặt khác, xét $\Delta AHC$ vuông tại $H$ ta có
$\sin \widehat{C}=\dfrac{AH}{AC}\approx \dfrac{1,97}{3,8}\approx \sin 31^\circ 14'$
Do đó $\widehat{C}\approx 31^\circ 14'$
Mà $\widehat{A}=180^\circ -\left( 70^\circ +31^\circ 14' \right)=78^\circ 46'$
Ta có $HC=AC.\cos \widehat{C}\approx 3,80.\cos 31^\circ 14'\approx 3,25$
Mà $BC=BH+HC=0,72+3,25=3,97$.
Giải tam giác $ABC$ biết $\widehat{B}=60^\circ , \, AB=3$ và $BC=4,5$.
Hướng dẫn giải:
Kẻ đường cao $AH \bot BC$.
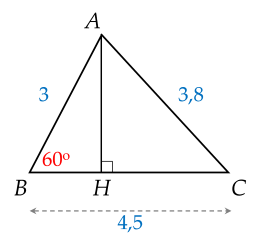
Xét $\Delta ABH$ vuông tại $H$ có $AH=AB.\sin \widehat{B}=3.\sin 60^\circ \approx 2,6$
Tương tự, xét $BH=AB.\cos \widehat{B}=3.\cos 60^\circ =1,5$
Mà $HC=BC-HB=4,5-1,5=3,0$
Theo định lí Pythagore ta có $AB^2=BH^2+AH^2=3^2+2,6^2=15,76$
Suy ra $AB=\sqrt{15,76}\approx 4,0$
Xét $\Delta AHC$ vuông tại $H$ ta có $\tan \widehat{ACH}=\dfrac{AH}{HC}\approx \dfrac{2,6}{3,0}\approx \tan 40^\circ 55'$
Do $\widehat{A}=180^\circ -\widehat{B}-\widehat{C}=180^\circ -\big( 60^\circ +40^\circ 55' \big)=79^\circ 5'$.
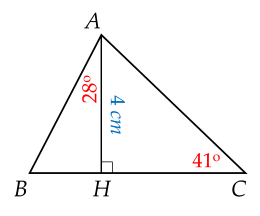
Trong hình vẽ, tính độ dài của mỗi đoạn thẳng sau:
a) $HB$ và $HC$.
b) $AH$ và $AC$.
Hướng dẫn giải:
a) Xét tam giác $ABH$ vuông tại $H$, ta có $HB=AH.\tan \widehat{BAH}=4.\tan 28^\circ \approx 2,1$ (cm)
Vì tam gaisc $AHC$ vuông tại $H$ nên $HC=AH.\cot \widehat{C}=4.\cot 41^\circ \approx 4,6$ (cm)
b) Xét tam giác $ABH$ vuông tại $H$, ta có
$\cos \widehat{BAH}=\dfrac{AH}{AB}$ hay $AB=\dfrac{AH}{\cos \widehat{BAH}}=\dfrac{4}{\cos 28{}^\circ }\approx 4,5$ (cm)
Vì tam giác $AHC$ vuông tại $H$ nên $\sin \widehat{C}=\dfrac{AH}{AC}$ hay $AC=\dfrac{AH}{\sin \widehat{C}}=\dfrac{4}{\sin 41^\circ } \approx 6,1$ (cm).
