Đề số 2 (thời gian: 90 phút) SVIP

Hướng dẫn giải:

a) \(\displaystyle \frac{x \sqrt{x}+1}{x+2 \sqrt{x}+1}: \frac{\sqrt{x}-x-1}{1-\sqrt{x}}=\frac{\sqrt{x}^3+1^3}{\sqrt{x}^2+2 \sqrt{x}+1}: \frac{\sqrt{x}^2-\sqrt{x}+1}{\sqrt{x}-1}\) (ĐK: \(x \ge 0, x \neq 1\))

\(\displaystyle =\frac{(\sqrt{x}+1)\left(\sqrt{x}^2-\sqrt{x}+1\right)}{(\sqrt{x}+1)^2} \cdot \frac{\sqrt{x}-1}{\sqrt{x}^2-\sqrt{x}+1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\).

b) Để đồ thị của hàm số đi qua gốc tọa độ $O(0;0)$ thì 

$0=-3.0-m+1 \Leftrightarrow m = 1$. 

Hướng dẫn giải:

a) Ta có: 

$x^2-x-6=0 \Leftrightarrow x^2 -3x+2x-6=0 \Leftrightarrow x(x-3)+2(x-3)=0$

$\Leftrightarrow (x-3)(x+2)=0$ \(\Leftrightarrow \left[ \begin{array}{l} x = 3\\ x = - 2. \end{array} \right.\)

b) Với $m=0$ phương trình (1) tương đương với: 

$2x=0 \Leftrightarrow x=0$ (loại)

Với $m \neq 0$, để phương trình (1) có hai nghiệm phân biệt thì

$\displaystyle \Delta'>0 \Leftrightarrow (m-1)^2-m^2>0 \Leftrightarrow -2m+1>0 \Leftrightarrow m< \frac{1}{2}$. 

Vậy phương trình (1) có hai nghiệm phân biệt khi $\displaystyle m \neq 0, m <\frac{1}{2}$.

Hướng dẫn giải:

Điều kiện: $\displaystyle x \neq \frac{3}{2}$.

\(\left\{\begin{array} { c } { x + y - x y = 0 } \\ \displaystyle { \frac { 2 y - x y } { 3 - 2 x } = 1 } \end{array} \Leftrightarrow \left\{\begin{array} { c } { x + y - x y = 0 } \\ { 2 x + 2 y - x y = 3 } \end{array} \Leftrightarrow \left\{\begin{array} { c } { x + y - x y = 0 } \\ { x + y = 3 } \end{array} \Leftrightarrow \left\{\begin{array}{c} x y=3 \\ x+y=3 \end{array}\right.\right.\right.\right.\)

Suy ra $x,y$ là nghiệm của phương trình $X^2-3X+3=0$. 

Phương trình này có $\Delta = 3^2-4.3=-3<0$ do đó phương trình này vô nghiệm suy ra phương trình đã cho vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

Hướng dẫn giải:

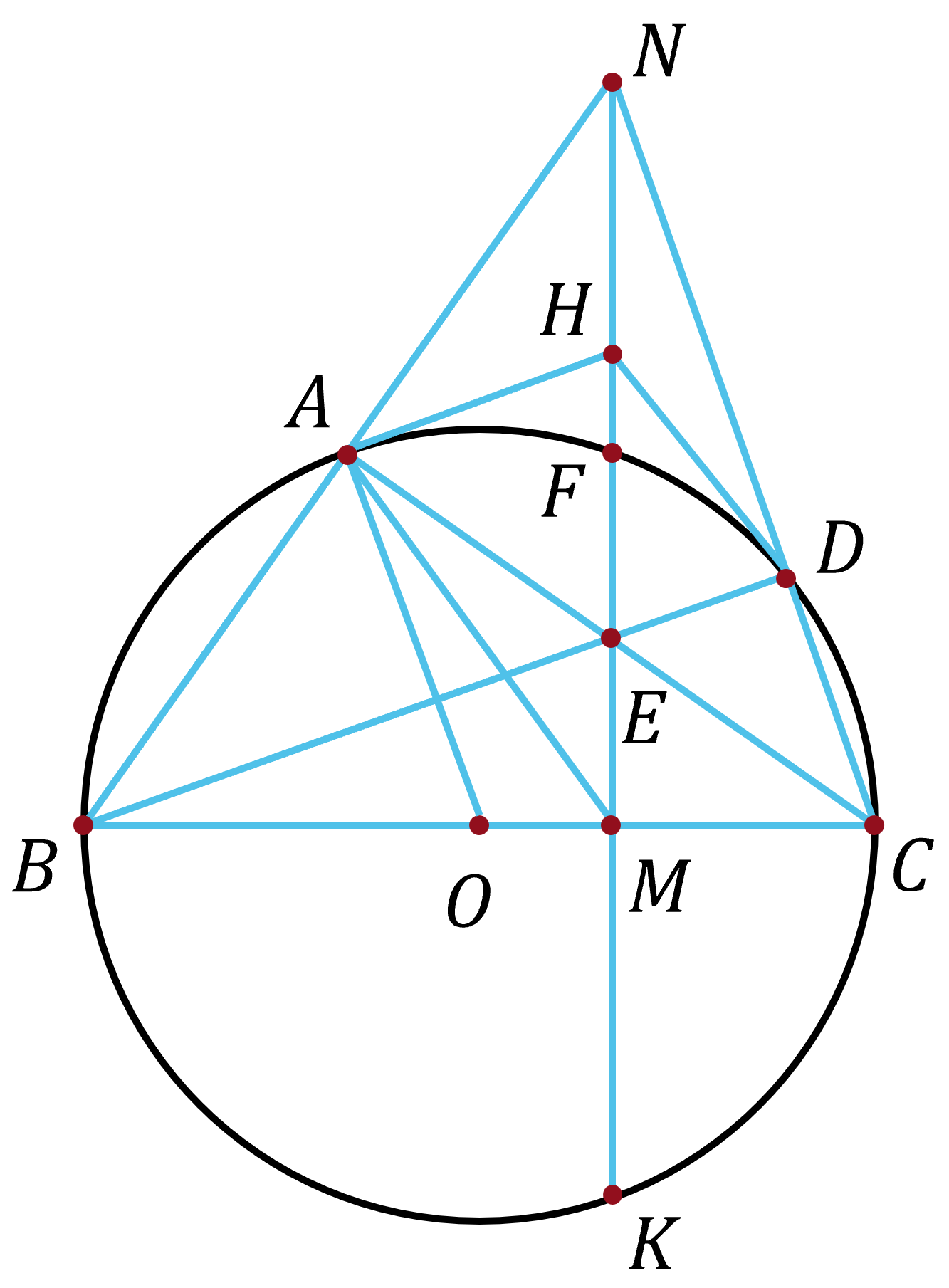
a) Xét tứ giác $ABME$ có: 

$\widehat{BAC}=90^\circ$ (góc nội tiếp chắn nửa đường tròn)

$\widehat{BME}=90^\circ$ (vì $EM \bot BC$) 

suy ra $\widehat{BAC}+\widehat{BME}=180^\circ$. 

Do đó tứ giác $ABME$ là tứ giác nội tiếp suy ra bốn điểm $A$, $B$, $M$, $E$ cùng thuộc một đường tròn.

Ta có: 

$\widehat{CAN}=\widehat{CMN}=90^\circ$ do đó $A$, $M$ cùng nhìn $CN$ dưới một góc vuông nên $A$, $M$ cùng thuộc đường tròn đường kính $CN$. 

Do đó bốn điểm $N$, $A$, $M$, $C$ cùng thuộc một đường tròn. 

b) Ta có tứ giác $ABME$ nội tiếp suy ra $\widehat{ABM}=\widehat{AEN}$.

Xét đường tròn $(O)$ có: 

$\widehat{ABM}=\widehat{HAC}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $AC$).

Suy ra $\widehat{AEN}=\widehat{HAC}$ suy ra tam giác $HAE$ cân tại $H$. 

c) Tam giác $NAE$ vuông tại $A$ có $AH=HE$ suy ra $H$ là trung điểm của $NE$, $\displaystyle AH=\frac{1}{2}NE$. 

Tam giác $NDE$ vuông tại $H$ có trung tuyến ứng với cạnh huyền $DH$ suy ra $\displaystyle DH=\frac{1}{2}NE$. 

Do đó $AH=DH$. 

Suy ra $\triangle AHO = \triangle ADO$ (c.c.c). 

Suy ra $\widehat{HDO}=\widehat{HAO} = 90^\circ$ nên $HD \bot OD$ do đó $HD$ là tiếp tuyến của đường tròn $(O)$. 

Hướng dẫn giải:

Điều kiện: \(x^5+x^3+x^2+1 \ge 0\).

Phương trình đã cho tương đương với: 

\(\begin{aligned} & 5 \sqrt{x^3\left(x^2+1\right)+\left(x^2+1\right)}=2 \sqrt{x^6+x^4+4 x^4+4 x^2+4 x^2+4} \\ & \Leftrightarrow 5 \sqrt{x^3\left(x^2+1\right)+\left(x^2+1\right)}=2 \sqrt{x^4\left(x^2+1\right)+4 x^2\left(x^2+1\right)+4\left(x^2+1\right)} \\ & \Leftrightarrow 5 \sqrt{\left(x^2+1\right)\left(x^3+1\right)}=2 \sqrt{\left(x^2+1\right)\left(x^4+4 x^2+4\right)} \\ & \Leftrightarrow 5 \sqrt{x^3+1}=2 \sqrt{\left(x^2+2\right)^2} \\ & \Leftrightarrow 5 \sqrt{x^3\left(x^2+1\right)+\left(x^2+1\right)}=2 \sqrt{x^6+x^4+4 x^4+4 x^2+4 x^2+4} \\ & \Leftrightarrow 5 \sqrt{x^3\left(x^2+1\right)+\left(x^2+1\right)}=2 \sqrt{x^4\left(x^2+1\right)+4 x^2\left(x^2+1\right)+4\left(x^2+1\right)} \\ & \Leftrightarrow 5 \sqrt{\left(x^2+1\right)\left(x^3+1\right)}=2 \sqrt{\left(x^2+1\right)\left(x^4+4 x^2+4\right)} \\ & \Leftrightarrow 5 \sqrt{x^3+1}=2 \sqrt{\left(x^2+2\right)^2}\\ & \Leftrightarrow 25(x+1)\left(x^2-x+1\right)=4\left(x^2+2\right)^2 \\ & \Leftrightarrow 25(x+1)\left[\left(x^2+2\right)-(x+1)\right]=4\left(x^2+2\right)^2 \\ & \Leftrightarrow-25(x+1)^2+25\left(x^2+2\right)(x+1)=4\left(x^2+2\right)^2 \\ & \Leftrightarrow 4\left(x^2+2\right)^2-25\left(x^2+2\right)(x+1)+25(x+1)^2=0 \\ & \Leftrightarrow 4\left(x^2+2\right)^2-20\left(x^2+2\right)(x+1)-5\left(x^2+2\right)(x+1)+25(x+1)^2=0 \\ & \Leftrightarrow 4\left(x^2+2\right)\left[\left(x^2+2\right)-5(x+1)\right]-5(x+1)\left[\left(x^2+2\right)-5(x+1)\right]=0 \\ & \Leftrightarrow\left[\left(x^2+2\right)-5(x+1)\right]\left[4\left(x^2+2\right)-5(x+1)\right]=0 \\ & \Leftrightarrow\left(x^2-5 x-3\right)\left(4 x^2-5 x+3\right)=0 \end{aligned}\)

\(\displaystyle \Leftrightarrow\left[\begin{array}{l} x^2-5 x-3=0 \\ 4 x^2-5 x+3=0 \end{array} \Leftrightarrow x=\frac{5 \pm \sqrt{37}}{2}\right.\).

Thử lại đều thỏa mãn. 

Vậy phương trình đã cho có tập nghiệm là \(\displaystyle S=\left\{\frac{5 \pm \sqrt{37}}{2}\right\}\).