Đề số 1 (thời gian: 90 phút) SVIP

Hướng dẫn giải:

1. Phương trình hoành độ giao điểm của $(P)$ và $(d)$: 

$x^2=-x+2 \Leftrightarrow x^2+x-2=0 \Leftrightarrow (x+2)(x-1)=0$

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1.\end{matrix}\right.\)

Với $x=1$ suy ra $y=1$ ta có điểm $A(1;1)$.

Với $x=-2$ suy ra $y=4$ ta có điểm $B(-2;4)$.

2. Gọi $F$ là giao điểm của $AB$ và trục $Oy$. 

Ta có $\displaystyle S_{AOB} =S_{AOF} + S_{FOB} = \frac{1}{2}(1+2).2=3$.

Hướng dẫn giải:

Gọi số chi tiết máy mỗi tổ sản xuất được trong tháng đầu lần lượt là $x$, $y$ (chi tiết) ($x,y \in \mathbb{N}^*$). 

Vì trong tháng đầu hai tổ sản xuất được $860$ chi tiết máy nên ta có phương trình: 

$x+y=860$ (1) 

Vì đến tháng thứ hai tổ I vượt mức \(15\%\), tổ hai vượt mức $10\%$ nên tháng thứ hai cả hai tổ sản xuất được $964$ chi tiết máy nên ta có phương trình:

$x+15\%x+y+10\%y=964 \Leftrightarrow 1,15x+1,1y=964$ (2)

Từ (1) và (2) ta có hệ phương trình: 

\(\left\{{}\begin{matrix}x+y=860\\1,15x+1,1y=964\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1,1x+1,1y=946\\1,15x+1,1y=964\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}0,05x=18\\x+y=860\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=360\\y=500.\end{matrix}\right.\) (thỏa mãn)

Vậy trong tháng đầu, tổ I sản xuất được $360$ chi tiết máy, tổ II sản xuất được $500$ chi tiết máy.

Hướng dẫn giải:

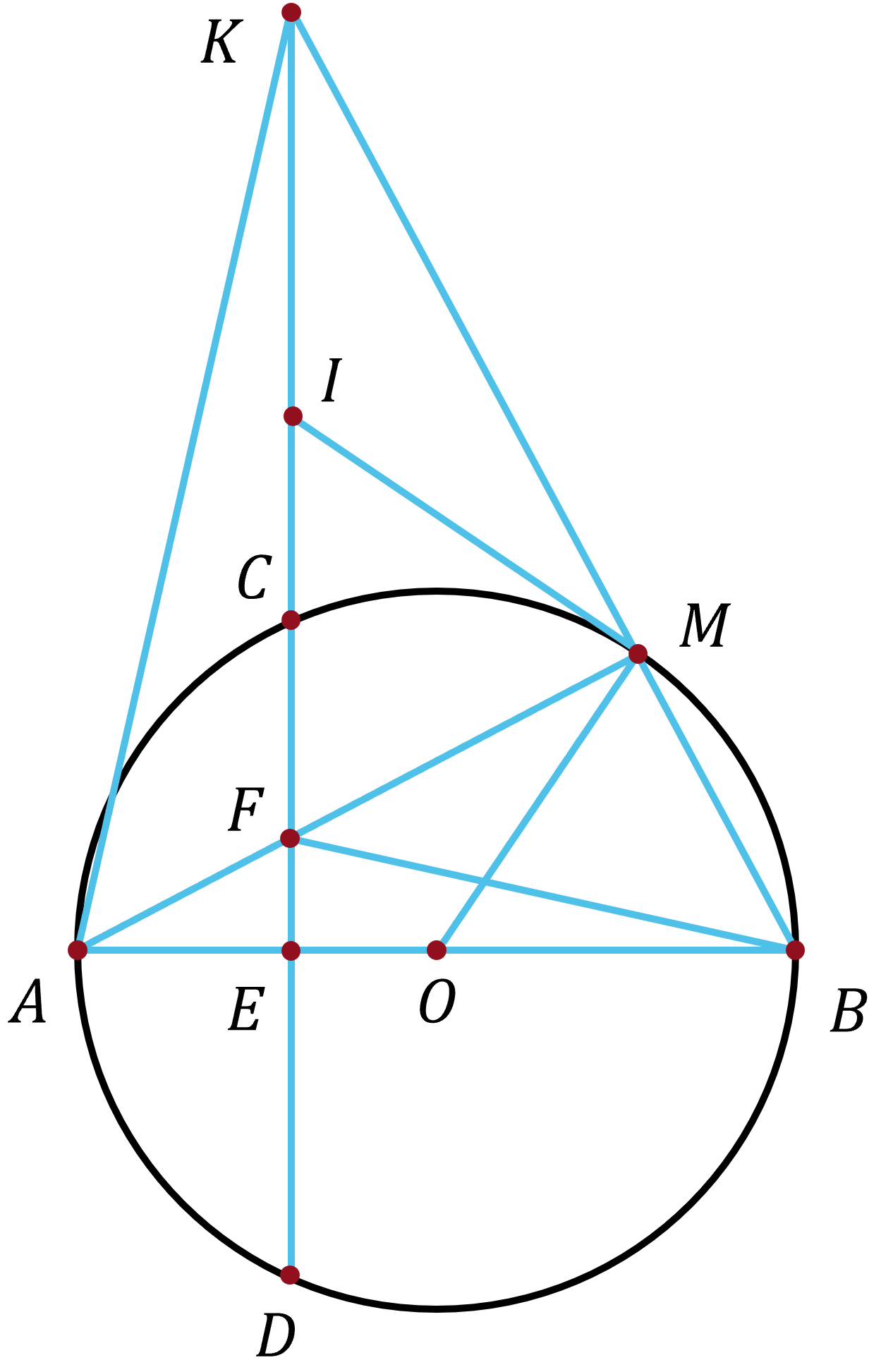
1. Ta có $\widehat{FEB}=\widehat{FMB}=90^\circ$ do đó $E$, $M$ cùng nhìn $FB$ dưới một góc $90^\circ$ nên $E$, $M$ cùng thuộc đường tròn đường kính $FB$ do đó tứ giác $BMFE$ nội tiếp.

2. Xét tam giác $AKB$ có: $KE \bot AB$, $AM \bot KB$ mà $F$ là giao điểm của $KE$, $AM$ do đó $F$ là trực tâm của tam giác $AKB$. 

Suy ra $BF \bot AK$.

Xét $\triangle AEF$ và $\triangle KEB$ có: 

$\widehat{AEF} = \widehat{KEB} (=90^\circ)$

$\widehat{EAF} = \widehat{EKB}$ (vì cùng phụ với $\widehat{ABM}$)

do đó $\triangle AEF \sim \triangle KEB$ (g.g) 

suy ra $\displaystyle \frac{EA}{EF} = \frac{EK}{EB} \Leftrightarrow EK.EF=EA.EB$.

3. Ta có: 

\(\left.\begin{array}{l} \widehat{I M K}=\widehat{O M A}\left(=90^{\circ}-\widehat{I M F}\right) \\ \widehat{M K I}=\widehat{O A M}\left(=90^{\circ}-\widehat{K B A}\right) \\ \widehat{O M A}=\widehat{O A M}(\text{vì } \triangle A O M \text { cân }) \end{array}\right\} \Rightarrow \widehat{I M K}=\widehat{M K I}\)

Do đó $\triangle IKM$ cân tại $I$ suy ra $IK=IM$. 

Tương tự ta cũng chứng minh được $\triangle IMF$ cân tại $I$ suy ra $IF=IM$. 

Từ đó ta suy ra được $IK=IF$.

Hướng dẫn giải:

Ta có: 

\(\displaystyle \frac{a}{1+9 b^2}=\frac{a+9 a b^2-9 a b^2}{1+9 b^2}=a-\frac{9 a b^2}{1+9 b^2} \geq a-\frac{9 a b^2}{6 b}=a-\frac{3}{2} a b\)

Chứng minh tương tự ta được:

$\displaystyle \frac{b}{1+9c^2} \ge b-\frac{3}{2}bc$, $\displaystyle \frac{c}{1+9a^2} \ge c-\frac{3}{2}ca$.

Cộng lại vế với vế ta được: 

\(\displaystyle \frac{a}{1+9 b^2}+\frac{b}{1+9 c^2}+\frac{c}{1+9 a^2} \ge (a+b+c)-\frac{3}{2}(a b+b c+c a)=1-\frac{3}{2}(a b+b c+c a)\).

Mặt khác ta có: 

\(a b+b c+c a \leq a^2+b^2+c^2=(a+b+c)^2-2(a b+b c+c a) =1-2(ab+bc+ca)\)

\(\displaystyle \Leftrightarrow ab+bc+ca \leq \frac{1}{3}\).

Suy ra \(\displaystyle \frac{a}{1+9 b^2}+\frac{b}{1+9 c^2}+\frac{c}{1+9 a^2} \ge 1-\frac{3}{2}.\frac{1}{3}=\frac{1}{2}\).

Dấu "$=$" xảy ra khi $\displaystyle a=b=c=\frac{1}{3}$.