Đề ôn tập chương 1 Toán 12 | Khảo sát hàm số và Ứng dụng

Câu 1 (1đ):

Hàm số $y=\sqrt{4-x^2}$ đồng biến trên khoảng nào sau đây?

(-2;+\infty)

.

(0;2)

.

(-2;2)

.

(-2;0)

.

Câu 2 (1đ):

Cho hàm số $y = f(x)$ có đạo hàm $f'(x)=x.(x-1)^2$ , $\forall x\in \mathbb{R}$ . Số điểm cực trị của hàm số đã cho là

0

.

3

.

2

.

1

.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình dưới đây:

Khi đó giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $[-10;10]$ bằng

\dfrac{14}{3}

.

\dfrac{11}{2}

.

-38

.

-2

.

Câu 4 (1đ):

Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2 x-1}{x-1}$ có phương trình là

x=2

.

y=1

.

x=1

.

y=2

.

Câu 5 (1đ):

Đồ thị của hàm số nào dưới đây là đường cong trong hình vẽ?

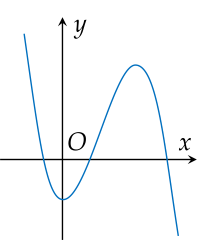
loading...

y={{x}^{4}}-2{{x}^{2}}-1

.

y=-{{x}^{4}}+2{{x}^{2}}-1

.

y={{x}^{3}}-3{{x}^{2}}-1

.

y=-{{x}^{3}}+3{{x}^{2}}-1

.

Câu 6 (1đ):

Cho hàm số $y=\dfrac{ax-2}{x+b}$ có đồ thị như hình dưới.

Khẳng định nào sau đây đúng?

b\lt 0\lt a

.

0\lt b\lt a

.

0\lt a\lt b

.

b\lt a\lt 0

.

Câu 7 (1đ):

Bảng biến thiên dưới đây là của hàm số nào?

y=x^3+6x^2+9x+4

.

y=x^3-6x^2+9x-4

.

y=-x^3+6x^2-9x+4

.

y=x^3-6x^2+9x

.

Câu 8 (1đ):

Hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ là hàm số $y = f'(x)$ . Biết đồ thị hàm số $f'(x)$ được cho như hình vẽ.

Hàm số $y = f(x)$ nghịch biến trên khoảng nào sau đây?

(-\infty ;0)

.

(0;+\infty)

.

\Big(\dfrac{1}{3};1\Big)

.

\Big(-\infty ;\dfrac{1}{3}\Big)

.

Câu 9 (1đ):

Cho hàm số $y=\dfrac{x^2+3x}{x-1}$ . Tọa độ điểm cực đại của đồ thị hàm số là

(3;9)

.

(2;10)

.

(-1;1)

.

(-3;0)

.

Câu 10 (1đ):

Giá trị lớn nhất của hàm số $y=-{{x}^{4}}+3{{x}^{2}}+1$ trên $\left[ 0;2 \right]$ là

-3

.

\dfrac{13}{4}

.

29

.

1

.

Câu 11 (1đ):

Số tiệm cận của đồ thị hàm số $y=\dfrac{2x+1}{2-x-x^2}$ là

1

.

4

.

3

.

2

.

Câu 12 (1đ):

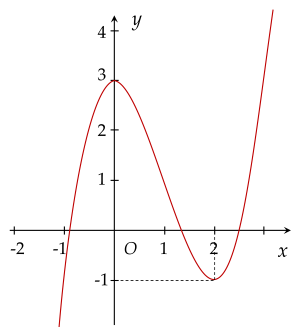
loading...

Đường cong của hình vẽ trên là của đường cong nào dưới đây?

y=-x^{3}+3 x^{2}+3

.

y=-x^{3}-3 x^{2}+3

.

y=x^{3}-3 x^{2}+3

.

y=x^{3}-3 x+3

.

Câu 13 (1đ):

Cho hàm số $y=f(x)$ xác định và liên tục trên khoảng $(-\infty ;\,+\infty)$ có bảng biến thiên như sau:

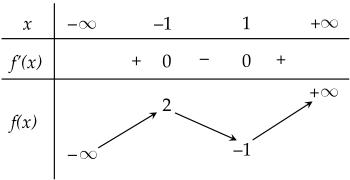
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số đồng biến trên khoảng $(-1;\,+\infty)$ .
b) Hàm số nghịch biến trên khoảng $(-1;\,1)$ .
c) Hàm số đạt cực đại tại $x=1$ .
d) Giá trị cực tiểu của hàm số là $-1$ .

Câu 14 (1đ):

Cho hàm số $y=f(x)$ liên tục trên đoạn $[-1;3]$ và có đồ thị như hình vẽ.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số $y=f(x)$ nghịch biến trên khoảng $(0;2)$ .
b) $\underset{[0;2]}{\mathop{\max}}f(x)=1.$
c) Gọi $M,m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn $[-1;3]$ . Giá trị của $M+m$ là $2$ .
d) Xét hàm số $g(x)=f(x+1)$ thì $\underset{[0;2]}{\mathop{\max}}g(x)=-3.$

Câu 15 (1đ):

Cho hàm số $y=f(x)=\dfrac{ax^2+bx+c}{x+d}$ có đồ thị là đường cong như hình vẽ dưới đây, biết đường tiệm xiên của đồ thị hàm số đi qua hai điểm $(0;1)$ và $(1;0)$ .

$hàm số $y=f(x)=\dfrac{ax^2+bx+c}{x+d}$ có đồ thị là đường cong$

(Nhấp vào ô màu vàng để chọn đúng / sai)

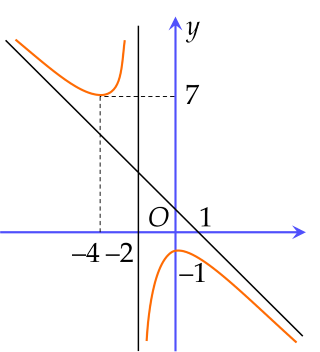
a) Khoảng cách từ $M(1;-8)$ đến đường thẳng đi qua các điểm cực trị của đồ thị hàm số bằng $\sqrt{5}$ .
b) Hàm số đồng biến trên khoảng $(-4;0)$ .
c) Ta có $a+b+c+d=-2$ .
d) Tập xác định của hàm số là $\mathbb{R}\backslash \{ 2 \}$ .

Câu 16 (1đ):

Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ.

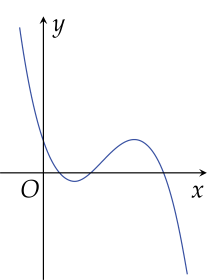
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $ab\lt 0$ .
b) Hàm số đã cho có hai cực trị.
c) $c$ và $d$ cùng dấu.
d) Đồ thị hàm số có $4$ giao điểm với trục hoành.

Câu 17 (1đ):

Một người nuôi cá thí nghiệm trong hồ. Người đó thấy rằng nếu mỗi đơn vị diện tích của mặt hồ có $n$ con cá thì trung bình mỗi con cá sau một vụ cân nặng $P(n)=480-20n$ (gam). Cần phải thả bao nhiêu cá trên mỗi đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?

Trả lời:

Câu 18 (1đ):

Cho hàm số $y=x^3-3x^2+1$ . Độ dài đoạn thẳng nối hai điểm cực trị của đồ thị hàm số đã cho là bao nhiêu đơn vị độ dài? Làm tròn đến chữ số thập phân thứ hai

Trả lời:

Câu 19 (1đ):

Một màn ảnh hình chữ nhật cao $1,4$ m được đặt ở độ cao $1,8$ m so với tầm mắt.

Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu mét sao cho góc nhìn lớn nhất. Làm tròn kết quả đến hàng phần mười.

Trả lời:

Câu 20 (1đ):

Một bể chứa $1\,000$ lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ $15$ gam muối cho mỗi lít nước với tốc độ $20$ lít/phút. Biết rằng nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số $f\left(t \right)$ , thời gian $t$ tính bằng phút. Phương trình tiệm cận ngang của đồ thị hàm số $y = f(t)$ là $y = a$ . Tính $a$ .

Trả lời:

Câu 21 (1đ):

Ban đầu bạn An ở vị trí điểm $A$ muốn đến điểm $C$ ở bên bờ sông. Biết rằng An đứng đối diện và cách chiếc cọc tại điểm $B$ một khoảng cách $10$ km. Khi sang sông, An sẽ đến vị trí điểm $M$ bất kì thuộc đoạn thẳng $BC$ .

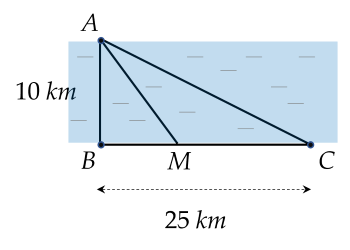
loading...

Biết trên sông, An di chuyển với vận tốc $30$ km/h và trên đất liền, An di chuyển với vận tốc $50$ km/h. Tính $5MB+3MC$ (đơn vị km) để bạn An đến vị trí điểm $C$ nhanh nhất?

Trả lời:

Câu 22 (1đ):

Một hộ sản xuất vải sấy Lục Ngạn mỗi ngày sản xuất được $x$ kg vải ( $6\lt x\lt 14$ ). Tổng chi phí sản xuất $x$ kg vải, tính bằng nghìn đồng, cho bởi hàm chi phí: $C(x)=x^3-3 x^2-19 x+300$ . Giả sử hộ sản xuất này bán hết sản phẩm mỗi ngày với giá $170$ nghìn đồng/kg. Hộ sản xuất này cần sản xuất và bán ra mỗi ngày bao nhiêu kg vải sấy để thu được lợi nhuận tối đa?

Trả lời:

Bài học cùng chủ đề

Đề số 2: Khảo sát hàm số và Ứng dụng SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề số 2: Khảo sát hàm số và Ứng dụng SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP