Đề ôn tập chương 1 Toán 12 | Khảo sát hàm số và Ứng dụng

Câu 1 (1đ):

Cho hàm số $y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-12x-1$ . Mệnh đề nào sau đây đúng?

Hàm số đồng biến trên khoảng

(-\infty ;4)

.

Hàm số đồng biến trên khoảng

(4;+\infty)

.

Hàm số nghịch biến trên khoảng

(-3;+\infty)

.

Hàm số đồng biến trên khoảng

(-3;4)

.

Câu 2 (1đ):

Biết hàm số $y=\dfrac{x+a}{x+1}$ ( $a$ là số thực cho trước, $a\ne 1$ ) có đồ thị như hình vẽ:

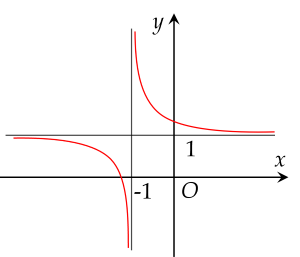
loading...

Mệnh đề nào dưới đây đúng?

y'>0,\,\forall x\in \mathbb{R}

.

y'<0,\,\forall x\in \mathbb{R}

.

y'>0,\,\forall x\ne -1

.

y'<0,\,\forall x\ne -1

.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-1)(2-x)$ , $\forall x\in \mathbb{R}$ . Điểm cực đại của hàm số là

y=1

.

y=-2

.

x=2

.

x=-1

.

Câu 4 (1đ):

Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ:

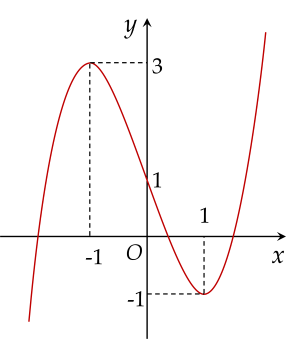
loading...

Trên đoạn $[0;1]$ , hàm số $y = f(x)$ đạt giá trị nhỏ nhất tại

x=0

.

x=2

.

x=-1

.

x=1

.

Câu 5 (1đ):

Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như sau:

Đồ thị hàm số $y=f\left(x \right)$ có bao nhiêu đường tiệm cận?

3

.

0

.

2

.

1

.

Câu 6 (1đ):

Trong các hàm số dưới đây, hàm số nào có đồ thị đi qua điểm $M(1;0)$ ?

y=x^3+3x^2-3

.

y=\dfrac{2x-2}{x^2-1}

.

y=(x-1)\sqrt{x-2}

.

y=x^4-3x^2+2

.

Câu 7 (1đ):

Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ.

Mệnh đề nào dưới đây đúng?

a\lt 0,\,b>0,\,c\lt 0,\,d\lt 0

.

a\lt 0,\,b\lt 0,\,c>0,\,d\lt 0

.

a\lt 0,\,b>0,\,c>0,\,d\lt 0

.

a\lt 0,\,b\lt 0,\,c\lt 0,\,d\lt 0

.

Câu 8 (1đ):

Ðồ thị dưới đây là của hàm số nào?

y=\dfrac{x-1}{2x+1}

.

y=\dfrac{x}{2x+1}

.

y=\dfrac{x+3}{2x+1}

.

y=\dfrac{x+1}{2x+1}

.

Câu 9 (1đ):

Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

loading...

y=x^3-3x+1

.

y=x^3-3x-1

.

y=-x^3+3x^2+1

.

y=-x^3-3x^2-1

.

Câu 10 (1đ):

Cho hàm số $y=\dfrac{-2}{x+1}$ có đồ thị là $(C)$ . Khẳng định nào dưới đây đúng?

(C)

chỉ có một tiệm cận.

(C)

có tiệm cận đứng là

x=1

.

(C)

có tiệm cận xiên là

y=x+1

.

(C)

có tiệm cận ngang là

y=0

.

Câu 11 (1đ):

Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như hình vẽ.

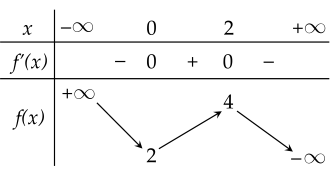
loading...

Điểm cực tiểu của đồ thị hàm số là

\left(4;2 \right)

.

\left(2;4 \right)

.

\left(0;2 \right)

.

\left(2;0 \right)

.

Câu 12 (1đ):

Gọi $M$ , $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\dfrac{x^2+5}{x-2}$ trên $\left[ -2;1 \right]$ . Giá trị của $M+2m$ bằng

-10

.

-14

.

-8

.

-2

.

Câu 13 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ.

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\underset{[0;2]}{\mathop{\max }}\,f(x)=4$ .
b) Hàm số $y=f(x)$ có giá trị lớn nhất là $4$ và giá trị nhỏ nhất là $0$ .
c) Hàm số $y=f(2\cos x)$ có giá trị lớn nhất là $4$ tại $x=\dfrac{\pi }{2}$ .
d) Trong khoảng $(-2;2)$ hàm số $y=f(f(x))$ có giá trị lớn nhất là $2$ .

Câu 14 (1đ):

Cho hàm số $y=\dfrac{x+3}{1-x}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đồ thị hàm số có tiệm cận đứng là $x=1$ .
b) Đồ thị hàm số có tiệm cận ngang là $y=-1$ .
c) Hàm số nghịch biến trên mỗi khoảng $\Big(-\infty ;\,1\Big)$ và $\Big(1;\,+\infty\Big)$ .
d) Hàm số không có cực trị.

Câu 15 (1đ):

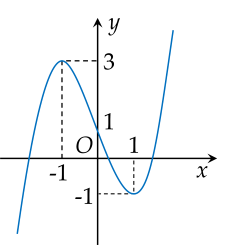
Cho hàm số $y = a x^{3}+b x^{2}+c x+d$ , $(a \neq 0)$ có đồ thị như hình vẽ:

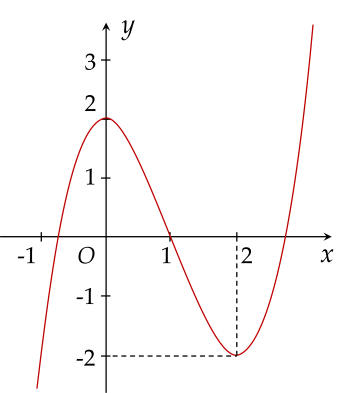
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điểm cực đại của đồ thị hàm số là $(2 ; 0)$ .
b) Hàm số đồng biến trên khoảng $(-\infty ; 0)$ .
c) Hệ số $c=0$ .
d) Đồ thị hàm số đi qua điểm $(4 ; 10)$ .

Câu 16 (1đ):

Cho hàm số $y=f(x)$ xác định và liên tục trên khoảng $(-\infty ;\,+\infty)$ có bảng biến thiên như sau:

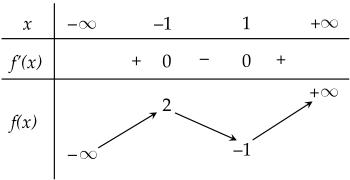
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số đồng biến trên khoảng $(-1;\,+\infty)$ .
b) Hàm số nghịch biến trên khoảng $(-1;\,1)$ .
c) Hàm số đạt cực đại tại $x=1$ .
d) Giá trị cực tiểu của hàm số là $-1$ .

Câu 17 (1đ):

Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số $y = h(x) = -\dfrac{1}{1\,320\,000}x^3 + \dfrac{9}{3\,520}x^2 -\dfrac{81}{44}x + 840$ với $0 \le x \le2\,000$ . Biết đỉnh của lát cắt dãy núi nằm ở độ cao $h$ (m) thuộc đoạn $[1\,000; 2\,000]$ . Tính $h$ . (Kết quả làm tròn đến hàng đơn vị)

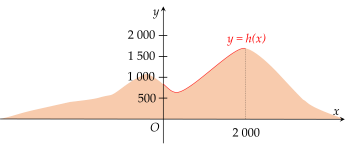
loading...

Trả lời:

Câu 18 (1đ):

Một cửa hàng cà phê sắp khai trương đang nghiên cứu thị trường để định giá bán cho mỗi cốc cà phê. Sau khi nghiên cứu, người quản lý thấy rằng nếu bán với giá $20$ $000$ đồng một cốc thì mỗi tháng trung bình sẽ bán được $2$ $000$ cốc, còn từ mức giá $20$ $000$ đồng mà cứ tăng giá thêm $1$ $000$ đồng thì sẽ bán ít đi $100$ cốc. Biết chi phí nguyên vật liệu để pha một cốc cà phê không thay đổi là $18$ $000$ đồng. Cửa hàng phải bán mỗi cốc cà phê với giá bao nhiêu nghìn đồng để đạt lợi nhuận lớn nhất?

Trả lời:

Câu 19 (1đ):

Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng $1$ m $^3$ . Chiều cao của bể là $5$ dm, các kích thước khác là $x$ m, $y$ m với $x>0$ và $y>0$ . Diện tích toàn phần của bể (không kể nắp) là hàm số $S(x)$ trên khoảng $\left(0;+\infty \right)$ .

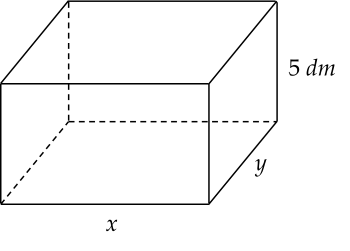
loading...

Đường tiệm cận xiên của đồ thị hàm số $S(x)$ là đường thẳng $y=ax+b$ . Tính $P=a^2+b^2$ .

Trả lời:

Câu 20 (1đ):

Một cửa hàng kinh doanh rau tươi ước tính doanh thu bởi hàm số $f(x)=x^2-29 \, 000x+1 \, 000 \, 100 \, 000$ (đồng) và tiền lãi thu được là $g(x)=1 \, 000x+100 \, 000$ (đồng) với $x$ (đồng) là giá bán cho mỗi kg rau tươi. Biết doanh thu bằng tổng tiền lãi và tiền vốn. Tìm giá bán mỗi kg rau tươi (đơn vị nghìn đồng) sao cho cửa hàng phải bỏ vốn ra ít nhất.

Trả lời:

Câu 21 (1đ):

Giả sử chi phí cho xuất bản $x$ cuốn tạp chí (gồm: lương cán bộ, công nhân viên, giấy in,...) được cho bởi công thức:

$C(x)=0,0001 x^2-0,2 x+10\,000$

trong đó $C(x)$ được tính theo đơn vị là vạn đồng ( $1$ vạn đồng $=10\,000$ đồng). Chi phí phát hành cho mỗi cuốn là $4$ nghìn đồng. Tỉ số $M(x)=\dfrac{T(x)}{x}$ được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản $x$ cuốn và tổng chỉ phí $T(x)$ (xuất bản và phát hành) cho $x$ cuốn tạp chí. Chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá $30\,000$ cuốn?

Trả lời:

Câu 22 (1đ):

Cho hàm số $y=x^3-3mx+1$ $(1)$ . Cho $A(2;3)$ , giá trị của $m$ để đồ thị hàm số $(1)$ có hai điểm cực trị $B$ và $C$ sao cho tam giác $ABC$ cân tại $A$ bằng bao nhiêu? Làm tròn đến chữ số thập phân thứ nhất.

Trả lời:

Bài học cùng chủ đề

Đề số 1: Khảo sát hàm số và Ứng dụng SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề số 1: Khảo sát hàm số và Ứng dụng SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP