Đề kiểm tra học kì I (đề số 1)

Câu 1 (1đ):

Bạn Long rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Long được thống kê lại ở bảng sau:

Thời gian (phút)	Số ngày
$[20;25)$	$4$
$[25;30)$	$3$
$[30;35)$	$5$
$[35;40)$	$1$
$[40;45)$	$2$

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

20

.

5

.

15

.

25

.

Câu 2 (1đ):

Trong không gian cho ba điểm $M,\,N,\,P$ phân biệt. Tổng $\overrightarrow{PM}+\overrightarrow{MN}$ là

\overrightarrow{MN}

.

\overrightarrow{NP}

.

\overrightarrow{NM}

.

\overrightarrow{PN}

.

Câu 3 (1đ):

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{a}=(-1 ; 3 ;-3)$ và $\overrightarrow{b}=(2 ; 1 ;-2)$ . Tọa độ của vectơ $\overrightarrow{b}-\overrightarrow{a}$ là

(1 ; 4 ;-5).

(3 ;-2 ; 1).

(1 ;-2 ; 3).

(3 ; 2 ;-1).

Câu 4 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho hình chữ nhật $OKMN$ .

loading...

Tọa độ đỉnh $M$ của hình chữ nhật là

M\left( -1;-\,2;\,-2 \right)

.

M\left( 1;\,2;\,2 \right)

.

M\left( 0;\,2;\,2 \right)

.

M\left( 1;2;\,0 \right)

.

Câu 5 (1đ):

Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?

y=\dfrac{4x+1}{x+2}

.

y=\dfrac{-2x+3}{x+1}

.

y=\dfrac{2x-3}{3x-1}

.

y=\dfrac{3x+4}{x-1}

.

Câu 6 (1đ):

Gọi $M, \, m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số $y=\sqrt{5-4x}$ trên đoạn $\left[ -1;\,1 \right]$ . Giá trị $M-m$ bằng

2

.

0

.

1

.

-1

.

Câu 7 (1đ):

Hàm số $y=x^3 - 2x^2 + x + 1$ nghịch biến trên khoảng nào dưới đây?

\Big(-\infty;\dfrac{1}{3}\Big)

.

\big(1;+\infty \big)

.

\Big(1 ; \dfrac13\Big)

.

\Big(\dfrac{1}{3}; 1\Big)

.

Câu 8 (1đ):

Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ $1$ đến dưới $6$ lượt đặt bàn, cột thứ hai biểu diễn số ngày có từ $6$ đến dưới $11$ lượt đặt bàn, ...

loading...

Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên là

9.

10.

7,5.

8,5.

Câu 9 (1đ):

Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ $Oxyz$ được thiết lập như hình vẽ dưới, cho biết $M$ là vị trí của máy bay, $OM=14, \,\widehat{NOB}=32^\circ, \, \widehat{MOC}=65^\circ$ .

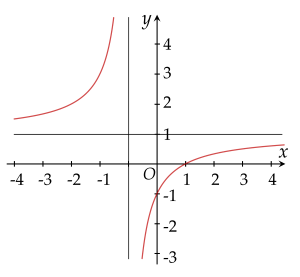
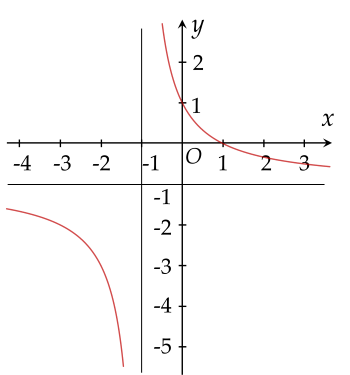
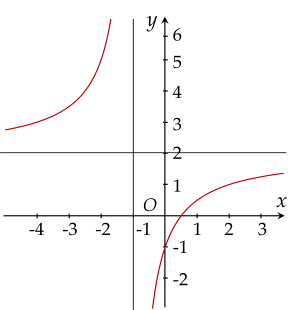
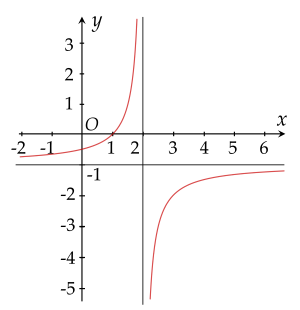
loading...

Tọa độ điểm $M$ là

M(10,8\,;\,6,7\,;\,5,9)

.

M(5,9\,;\,6,7\,;\,10,8)

.

M(6,7\,;\,10,8\,;\,-5,9)

.

M(6,7\,;\,10,8\,;\,5,9)

.

Câu 10 (1đ):

Cho hàm số $y=\dfrac{ax+b}{x+1}$ có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?

loading...

ab<0

.

ab>0

.

a<b

.

b<a<0

.

Câu 11 (1đ):

Một nhà máy sản xuất linh kiện điện tử thống kê được rằng trung bình một tổ sản xuất với $x$ người thì số sản phẩm sản xuất được trong một thời gian cố định được tính bẳng công thức $P(x)=\dfrac{5\,000x}{4x+25}$ . Xem $y=P(x)$ là một hàm số xác định trên $\left[ 0;+\infty \right)$ , khi đó tiệm cận ngang của đồ thị hàm số đó là

x=1\,250

.

y=1\,250

.

x=25

.

y=25

.

Câu 12 (1đ):

Cho hàm số $y=f(x)$ có đồ thị của hàm số $y={f}'(x)$ như hình vẽ.

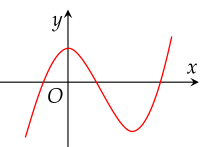
loading...

Số điểm cực trị của hàm số $y=f(x)$ là

4

.

1

.

2

.

3

.

Câu 13 (1đ):

Cho bảng số liệu ghép nhóm thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021 – 2022 cho kết quả sau:

Số thẻ vàng	Tần số
$[40 ; 50)$	$2$
$[50 ; 60)$	$5$
$[60 ; 70)$	$7$
$[70 ; 80)$	$5$
$[80 ; 90)$	$0$
$[90 ; 100)$	$0$
$[100 ; 110)$	$1$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Cỡ mẫu của mẫu số liệu trên là $20.$
b) Khoảng biến thiên của mẫu số liệu trên là $50$ .
c) Tứ phân vị của thứ nhất của mẫu số liệu gốc thuộc vào nhóm $[50 ; 60)$ .
d) Khoảng tứ phân vị của mẫu số liệu trên là $\Delta_{Q}=26$ .

Câu 14 (1đ):

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ thỏa mãn $| \overrightarrow{a}|=2$ ; $| \overrightarrow{b}|=5$ , góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng $60^\circ$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $(\overrightarrow{a},\,-2\overrightarrow{b})=60^\circ$ .
b) $\overrightarrow{a}.\overrightarrow{b}=5$ .
c) $\| \overrightarrow{a}-2\overrightarrow{b}\|=84$ .
d) Biết vectơ $\overrightarrow{v}$ ngược hướng với vectơ $\overrightarrow{a}-2\overrightarrow{b}$ và $\| \overrightarrow{v} \|=4\sqrt{21}$ . Gọi $\alpha$ là góc giữa hai vectơ $\overrightarrow{v}$ và $\overrightarrow{a}$ . Khi đó $\cos \alpha =\dfrac{\sqrt{21}}{84}$ .

Câu 15 (1đ):

Một vật chuyển động có phương trình quãng đường tính bằng mét phụ thuộc thời gian $t$ tính bằng giây được biểu thị bởi hàm số $f(t)=-t^{3}+9 t^{2}+21 t$ (m).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Quãng đường mà vật đi được sau $2$ s kể từ lúc bắt đầu chuyển động là $70$ m .
b) Vận tốc lớn nhất của vật thể là $21$ (m/s).
c) Vận tốc của vật tăng từ lúc bắt đầu chuyển động đến giây thứ $3.$
d) Kể từ lúc bắt đầu chuyển động đến khi dừng hẳn, vật đi được quãng đường là $250$ m.

Câu 16 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số đã cho đồng biến trên $\mathbb{R}$ .
b) Phương trình $y=0$ có $3$ nghiệm phân biệt.
c) Hàm số đã cho không có cực trị.
d) Số đường tiệm cận của đồ thị hàm số là $3$ .

Câu 17 (1đ):

Hằng ngày bà Giang đều đi xe máy từ nhà đến cơ quan. Bảng thống kê dưới đây cho biết thời gian bà Giang đi xe máy từ nhà đến cơ quan.

Nhóm	Tần số
$[20;26)$	$4$
$[26;32)$	$4$
$[32;38)$	$12$
$[38;44)$	$10$

Tính phương sai của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến chữ số hàng phần trăm)

Trả lời:

Câu 18 (1đ):

Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm $O$ trên trần nhà lần lượt buộc vào ba điểm $A,\,B,\,C$ trên đèn tròn sao cho tam giác $ABC$ đều. Độ dài $L$ của ba đoạn dây $OA,\,OB,\,OC$ đều bằng $l$ (m). Trọng lượng của chiếc đèn là $27$ N và bán kính của chiếc đèn là $0,5$ m.

loading...

Xác định chiều dài tối thiểu của mỗi sợi dây. Biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là $12$ N. (Chiều dài tính theo đơn vị cm và làm tròn đến chữ số thập phân thứ nhất)

Trả lời:

Câu 19 (1đ):

Một ngọn hải đăng đặt tại vị trí $A$ có khoảng cách đến bờ biển $AB = 5$ km. Trên bờ biển có một cái kho ở vị trí $C$ cách $B$ một khoảng $7$ km. Người canh hải đăng có thể chèo đò từ $A$ đến $M$ trên bờ biển với vận tốc $4$ km/h rồi đi bộ đến $C$ với vận tốc $6$ km/h. Vị trí của điểm $M$ cách $B$ một khoảng bao nhiêu ki-lô-mét để người đó đi đến kho nhanh nhất? (kết quả làm tròn đến hàng phần mười)

loading...

Trả lời:

Câu 20 (1đ):

Trong bài thực hành của môn huấn luyện quân sự có tình huống chiến sĩ phải bơi qua một con sông để tấn công một mục tiêu ở phía bờ bên kia sông. Biết rằng lòng sông rộng $100$ m và vận tốc bơi của chiến sĩ bằng một nửa vận tốc chạy trên bờ. Nếu như dòng sông là thẳng, mục tiêu ở cách chiến sĩ $1$ km theo đường chim bay thì người chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? (kết quả làm tròn đến hàng đơn vị)

loading...

Trả lời:

Câu 21 (1đ):

Tìm giá trị lớn nhất của tham số thực $m$ để hàm số $y=\dfrac{x^{3} }{3} -x^{2} -mx+1$ đồng biến trên tập xác định.

Trả lời:

Câu 22 (1đ):

Cho tứ diện $A B C D$ . Gọi $M$ và $N$ lần lượt là trung điểm của $A B$ và $C D$ . Tìm giá trị $k$ trong đẳng thức vectơ $\overrightarrow{M N}=k(\overrightarrow{A D}+\overrightarrow{B C})$ . (ghi kết quả dưới dạng số thập phân)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP