Đề kiểm tra giữa học kì I toán 12 cấu trúc mới mới nhất

Câu 1 (1đ):

Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=x(x-2),\,\forall x\in \mathbb{R}$ . Hàm số $y=f(x)$ nghịch biến trên khoảng nào dưới đây?

(0;\,2)

.

(0;\,+\infty)

.

(-\infty ;\,0)

.

(2;\,+\infty)

.

Câu 2 (1đ):

Cho hàm số $y=f(x )$ có bảng biến thiên như sau:

Giá trị cực đại của hàm số bằng

2

.

6

.

0

.

4

.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ có đồ thị trên đoạn $[-3;3]$ như hình vẽ.

Cho hàm số $y=f(x)$ có đồ thị trên đoạn $[-3;3]$

Hàm số đã cho đồng biến trên khoảng nào sau đây?

(0;2)

.

(-1;0)

.

(-3;-1)

.

(1;3)

.

Câu 4 (1đ):

Giá trị lớn nhất của hàm số $y={{x}^{3}}-2{{x}^{2}}-7x+1$ trên đoạn $\left[ -2;1 \right]$ là

3

.

5

.

4

.

6

.

Câu 5 (1đ):

Đồ thị hàm số nào sau đây nhận đường thẳng $x=2$ làm đường tiệm cận đứng?

y=\dfrac{2x}{x-2}

.

y=x-2-\dfrac{2}{x}

.

y=\dfrac{2x}{x+2}

.

y=2

.

Câu 6 (1đ):

Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

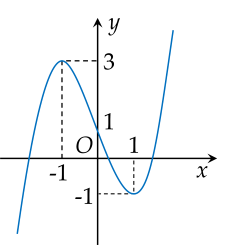
loading...

y=x^3-3x+1

.

y=x^3-3x-1

.

y=-x^3+3x^2+1

.

y=-x^3-3x^2-1

.

Câu 7 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Số nghiệm của phương trình $f(x)-2=0$ là

2

.

3

.

0

4

.

Câu 8 (1đ):

Tiếp tuyến của đồ thị hàm số $y=\dfrac{x^3}{3}-2x^2+3x+1$ song song với đường thẳng $y=3x+1$ có phương trình là

y=3x-1

.

y=3x-\dfrac{29}{3}

,

y=3x+1

.

y=3x+\dfrac{29}{3}

.

y=3x-\dfrac{29}{3}

.

Câu 9 (1đ):

Trong các hàm số dưới đây, hàm số nào có đồ thị đi qua điểm $M(1;0)$ ?

y=x^3+3x^2-3

.

y=\dfrac{2x-2}{x^2-1}

.

y=(x-1)\sqrt{x-2}

.

y=x^4-3x^2+2

.

Câu 10 (1đ):

Số lượng sản phẩm của công ty bán được trong $x$ (tháng) được tính bởi công thức $S(x)=300\Big(2+\dfrac{4}{x+2} \Big)$ với $x\ge 1$ . Xem $y=S(x)$ là một hàm số xác định trên $\left[ 1;+\infty \right)$ , khi đó tiệm cận ngang của đồ thị hàm số đó là

y=2\,400

.

x=300

.

y=600

.

x=600

.

Câu 11 (1đ):

Các giá trị của $m$ để hàm số $y=mx-\sin x+3$ đồng biến trên $\mathbb{R}$ là

m\ge -1

.

m\ge 1

.

m=1

.

m\lt 1

.

Câu 12 (1đ):

Giá trị của tham số $m$ để đồ thị hàm số $y=\dfrac{(m+1)x-5m}{2x-m}$ có tiệm cận ngang là đường thẳng $y=1$ là

m=-1

.

m=2

.

m=1

.

m=\dfrac{1}{2}

.

Câu 13 (1đ):

Cho hàm số $y=f(x)$ liên tục và có đồ thị trên đoạn $[-2 ; 4]$ như hình vẽ.

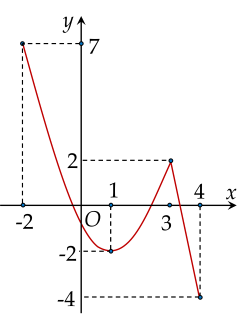
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Trên đoạn $[-2 ; 4]$ , đồ thị hàm số $y = f(x)$ có $2$ điểm cực trị.
b) Giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;2]$ là $-2$ .
c) Giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[1;4]$ là $-4$ .
d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;4]$ là $11$ .

Câu 14 (1đ):

Cho hàm số $y=f(x )=\dfrac{x^2-2x+3}{2x-1}$ biết đồ thị hàm số có tiệm cận xiên là đường thẳng $\Delta:y=ax+b$ và tiệm cận đứng là đường thẳng $x={{x}_{0}}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giá trị của biểu thức $S=4a-3b$ lớn hơn $4$ .
b) Giá trị nhỏ nhất của hàm số $y=ax+b$ trên $[ -4;-1]$ lớn hơn $-3$ .
c) Gọi điểm $M(4x_0;2a)$ , độ dài của $\overrightarrow{OM}$ bằng $5$ .
d) Gọi $A=\Delta\cap Ox,\,B=\Delta\cap Oy$ và $C=Ox\cap x_0$ ta có $S_{ABC}\lt 0,5$ .

Câu 15 (1đ):

Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong $t$ giờ được cho bởi hàm số có công thức $c(t)=\dfrac{t}{t^2+1}$ (mg/L).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nồng độ thuốc trong máu của bệnh nhân sau $3$ giờ là $c(3)=\dfrac{3}{10}$ (mg/L).
b) Đạo hàm của hàm số $c(t)=\dfrac{t}{t^2+1}$ là $c'(t)=\dfrac{1-t^2}{(t^2+1)^2}$ .
c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng $t\in (0;\,2)$ .
d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi $t=\dfrac{1}{2}$ .

Câu 16 (1đ):

Cho hàm số $y=f(x)=\dfrac{x^2-x+2}{x-2}$ có đồ thị $(C)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đường thẳng $y=x+1$ là tiệm cận xiên của đồ thị $(C)$ .
b) Đồ thị $(C)$ có tiệm cận đứng là đường thẳng $x=2$ ,
c) Đồ thị $(C)$ đi qua điểm $M(0;2)$ .
d) Đường thẳng $y=m$ cắt đồ thị $(C)$ tại hai điểm phân biệt khi $-1\lt m\lt 7$ .

Câu 17 (1đ):

Tại một công ty sản xuất đồ chơi an toàn cho trẻ em, công ty phải chi $40\,000$ USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi $A$ , công ty phải trả $6$ USD cho nguyên liệu ban đầu và nhân công. Gọi $x$ , ( $x \ge 1$ ) là số đồ chơi $A$ mà công ty đã sản xuất và $P(x)$ (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất $x$ đồ chơi $A$ . Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi $A$ là $F(x)=\dfrac{P(x)}{x}$ . Xem $y = F(x)$ là hàm số theo $x$ xác định trên nửa khoảng $\left[ 1;+\infty \right)$ có phương trình đường tiệm cận ngang là $y = b$ . Tính $b$ .

Trả lời:

Câu 18 (1đ):

Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số $y = f(t)=\dfrac{5\,000}{1+5 \mathrm{e}^{-t}}, \, t \geq 0,$ trong đó thời gian $t$ (năm) được tính kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm $f'(t)$ sẽ biểu thị tốc độ bán hàng. Sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất? (làm tròn kết quả tới chữ số hàng phần mười)

Trả lời:

Câu 19 (1đ):

Giả sử chi phí tiền xăng $C$ (đồng) phụ thuộc tốc độ trung bình $v$ (km/h) theo công thức:

$C(v)=\dfrac{16\,000}{v}+\dfrac{5}{2}v$ $(0\lt v\le 120)$

Để biểu diễn trực quan sự thay đổi của $C(v)$ theo $v$ , người ta đã vẽ đồ thị hàm số $C(v)$ như hình bên.

Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?

Trả lời:

Câu 20 (1đ):

Một xí nghiệp $A$ chuyên cung cấp sản phẩm $S$ cho nhà phân phối $B$ . Hai bên thỏa thuận rằng, nếu đầu tháng $B$ đặt hàng $x$ tạ sản phẩm $S$ thì giá bán mỗi tạ sản phẩm $S$ là $P(x)=6-0,0005x^2$ (triệu đồng) $(x\le 40)$ . Chi phí $A$ phải bỏ ra cho $x$ tạ sản phẩm $S$ trong một tháng là $C(x)=10+3,5x$ (triệu đồng) và mỗi sản phẩm bán ra phải chịu thêm mức thuế là $1$ triệu đồng. Trong một tháng $B$ cần đặt hàng bao nhiêu tạ sản phẩm $S$ thì $A$ có được lợi nhuận lớn nhất, kết quả làm tròn đến hàng phần mười.

Trả lời:

Câu 21 (1đ):

Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình vẽ bên dưới.

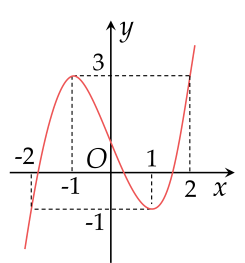
loading...

Phương trình $f\left[2-f(x) \right]=0$ có bao nhiêu nghiệm?

Trả lời:

Câu 22 (1đ):

Cho hàm số $y=f(x)$ có đồ thị của hàm số $y=f'(x)$ được cho như hình vẽ.

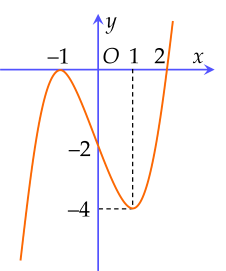
Hàm số $y=-2f(2-x)+x^2$ nghịch biến trên khoảng $(a;\,b)$ với $a$ , $b$ là các số nguyên. Tổng $a + b$ có giá trị bằng bao nhiêu?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP