Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì II (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=f(x) liên tục trên R và có một nguyên hàm là hàm số F(x), k∈N\{0}. Mệnh đề nào dưới đây sai?
Họ nguyên hàm của hàm số f(x)=ex−1 là
Hàm số F(x)=4x+x1 là một nguyên hàm của hàm số nào sau đây?
Giả sử F(x) là một nguyên hàm của hàm số f(x) trên đoạn [0;1]. Biết 0∫1f(x)dx=1 và F(0)=2, giá trị của F(1) bằng
Trong không gian Oxyz, mặt phẳng nào dưới đây chứa trục Oy?
Trong không gian với hệ trục tọa độ Oxyz. Bán kính r của mặt cầu (S) có tâm I(2;1;−1) và tiếp xúc với mặt phẳng (α):2x−2y−z+3=0 là
Trong không gian Oxyz, mặt phẳng (α):2x+3y+−1z=1 có một vectơ pháp tuyến là
Cho F(x) là một nguyên hàm của f(x)=x3x−2. Nếu F(−1)=3 thì F(x) bằng
Tích phân a∫b(1+sinx)dx với a<b có giá trị là
Cho 0∫1(x+2)2xdx=a+bln2+cln3 với a,b,c là các số hữu tỉ. Giá trị của biểu thức 3a+b+c bằng
Trong không gian Oxyz, cho đường thẳng Δ:2x+2=−2y=1z−1 và mặt phẳng (Q):x−y+3z=0. Phương trình mặt phẳng (P) đi qua điểm A(1;2;0), song song với đường thẳng Δ và vuông góc với mặt phẳng (Q) là
Trong không gian Oxyz, cho hai điểm A(0;2;−3) và B(4;−4;1). Gọi M là trung điểm của AB. Phương trình mặt phẳng trung trực của OM là
Cho (H) là hình phẳng giới hạn bởi 41 cung tròn có bán kính R=2, đường cong y=4−x và trục hoành, x=3.
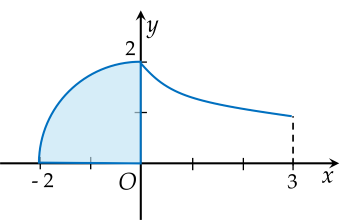
| a) Công thức tính diện tích hình quạt trên hình theo tích phân là −2∫04−x2dx |
|
| b) Diện tích hình phẳng (H) gần bằng 6,5. |
|
| c) Thể tích nửa khối cầu bán kính R=2 là 16π. |
|
| d) Thể tích V khối tạo thành khi cho (H) quay quanh Ox là 677π. |
|
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;3;−1),B(4;1;0),C(4;7;3).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Vectơ n=[AB,AC] là một vectơ pháp tuyến của mặt phẳng ABC. |
|
| b) Độ dài các cạnh tam giác ABC lần lượt là AB=3,AC=6,BC=4. |
|
| c) Tọa độ chân đường phân giác của BAC xuống BC là E(4;3;1). |
|
| d) Mặt phẳng đi qua điểm A, tâm đường tròn nội tiếp tam giác ABC và vuông góc với mặt phẳng (ABC) có phương trình (P):x−4y−z−9=0. |
|
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t)=4t m/s, trong đó thời gian t tính bằng giây. Sau khi chuyển động được 10 giây thì ô tô gặp chuớng ngại vật và người tài xế phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với vận tốc v2(t) và gia tốc là a=−3 m/s2 cho đến khi dừng hẳn.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Quãng đường ô tô chuyển động nhanh dần đều là 200 m. |
|
| b) Vận tốc của ô tô tại thời điểm người tài xế phanh gấp là 40 m/s. |
|
| c) Thời gian từ lúc ô tô giảm tốc độ cho đến khi dừng hẳn là 40 giây. |
|
| d) Tổng quãng đường ô tô chuyển động từ lúc xuất phát đến khi dừng hẳn là khoảng 650,7 m. |
|
Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho h′(t)=3at2+bt (m3/s) và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là 150 m3. Sau 10 giây thì thể tích nước trong bể là 1100 m3. Thể tích nước trong bể sau khi bơm được 20 giây là bao nhiêu m3? (Làm tròn kết quả đến chữ số hàng đơn vị)
Trả lời:
Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là 25 m/s, gia tốc trọng trường là 9,8 m/s2. Quãng đường viên đạn đi được từ lúc bắn cho đến khi chạm đất là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
Một ô tô đang chuyển động đều với vận tốc 10 m/s thì gặp chướng ngại vật, người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t)=−2t+10 (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quãng đường ô tô di chuyển được trong 8 giây cuối cùng.
Trả lời:
Trong không gian Oxyz, cho ba điểm A(2;0;0),B(0;1;0),C(0;0;−3). Gọi H là trực tâm tam giác ABC. Độ dài OH có dạng ba (là phân số tối giản có mẫu dương). Tính T=a+b.
Trả lời:
Một mảnh vườn hình tròn tâm O bán kính 6 m. Người ta cần trồng cây trên dải đất rộng 6 m nhận O làm tâm đối xứng, biết kinh phí trồng cây là 70 nghìn đồng/m2. Cần bao nhiêu tiền để trồng cây trên dải đất đó (số tiền được làm tròn đến hàng đơn vị)?
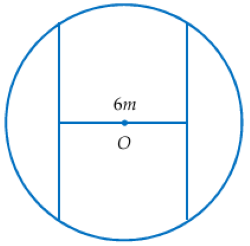
Trả lời: nghìn đồng
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng Δ:3x−1=−2y+2=1z−3 và mặt phẳng (P):x+y−z−1=0. Mặt phẳng (Q) đối xứng với (P) qua Δ có phương trình là ax+by+cz+d=0, trong đó a, b, c, d nguyên dương; a và b nguyên tố cùng nhau. Tính a+b+c+d.
Trả lời:
