Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hình hộp ABCD.A′B′C′D′ có đáy ABCD hình bình hành tâm O. Khi đó 2.AO bằng vectơ nào sau đây?
Trong không gian Oxyz, cho hai điểm A(1;1;−2) và B(3;−1;2). Tọa độ của vectơ BA là
Trong không gian với hệ toạ độ Oxyz, cho vectơ u=2i−3j+6k. Độ dài của vectơ u là
Cho hàm số y=31x3−21x2−12x−1. Mệnh đề nào sau đây đúng?
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên sau:

Khẳng định nào sau đây đúng?
Đường tiệm cận ngang của đồ thị hàm số y=4x2+12x−1 là
Đường cong nào dưới đây là đồ thị của hàm số y=1−xx+1?




Cho hàm số y=x−22x−3 có đồ thị là (C). Tiếp tuyến của đồ thị cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A,B sao cho côsin góc ABI bằng 174, với I(2;2). Khi đó, phương trình tiếp tuyến của đồ thị hàm số có dạng
Một ứng dụng của hàm số trong vật lí là hệ số tương đối tính Lorentz được cho bởi công thức γ(v)=1−c2v21, với v là vận tốc tương đối giữa các hệ quy chiếu quán tính, c là tốc độ ánh sáng trong chân không. Hàm này được sử dụng trong thuyết tương đối đặc biệt của Einstein để mô tả các hiệu ứng tương đối tính có đồ thị dưới đây:
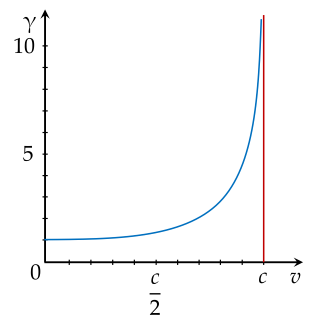
Đồ thị hàm số đó có tiệm cận đứng là
Giá trị lớn nhất của hàm số y=2x3+3x2−12x+2 trên đoạn [−1;2] là
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(−1;1;−3), B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
Cho hàm số y=f(x) xác định trên R\{x2} và có bảng xét dấu của đạo hàm như sau:
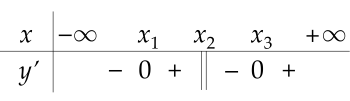
Số điểm cực trị của hàm số y=f(x) là
Trong không gian, cho tứ diện ABCD. Trên cạnh AD và BC lần lượt lấy các điểm M,N sao cho AM=3MD và BN=3NC. Gọi P,Q lần lượt là trung điểm AD và BC.

| a) PQ=AC+DB. |
|
| b) MN=MA+AC+CN. |
|
| c) MN=MD+DB+BN. |
|
| d) BD,AC,MN không đồng phẳng. |
|
Cho hàm số y=f(x) xác định và liên tục trên R, có bảng biến thiên như hình vẽ:
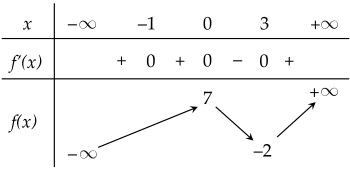
| a) Hàm số y=f(x) đồng biến trên khoảng (−2;+∞). |
|
| b) Hàm số y=f(x) đồng biến trên khoảng (−∞;0). |
|
| c) Hàm số y=f(x) có ba điểm cực trị. |
|
| d) Hàm số y=f(x) đạt cực đại tại điểm y=7 và đạt cực tiểu tại điểm y=−2. |
|
Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng 480 nghìn đồng mỗi giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, khi v=10 km/h thì phần thứ hai bằng 30 nghìn đồng mỗi giờ.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Khi vận tốc v=10 (km/h) thì chi phí nguyên liệu cho phần thứ nhất trên mỗi km đường sông là 48000 đồng. |
|
| b) Hàm số xác định tổng chi phí nguyên liệu trên mỗi km đường sông với vận tốc x km/h là f(x)=x480+0,03x3. |
|
| c) Khi vận tốc v=30 km/h thì tổng chi phí nguyên liệu trên mỗi km đường sông là 43000 đồng. |
|
| d) Vận tốc của tàu để tổng chi phí nguyên liệu trên mỗi km đường sông nhỏ nhất là v=20 km/h. |
|
Cho hàm số y=f(x)=(4−x2)2+1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số đã cho có 3 điểm cực trị. |
|
| b) Tập giá trị của hàm số là R. |
|
| c) Trên đoạn [−2;1], giá trị nhỏ nhất của hàm số là 1. |
|
| d) Trên khoảng [0;+∞), giá trị lớn nhất của hàm số là 17. |
|
Trong hóa học cấu tạo của phân tử ammoniac (NH3) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (N) và đáy là tam giác H1H2H3 với H1,H2,H3 là vị trí của ba nguyên tử hydrogen (H). Góc tạo bởi liên kết H−N−H, có hai cạnh là hai đoạn thẳng nối N với hai trong ba điểm H1,H2,H3 (chẳng hạn như H1NH2) , được gọi là góc liên kết của phân tử NH3. Góc này xấp xỉ 120∘. Trong không gian Oxyz, cho một phân tử NH3 được biểu diễn bởi hình chóp tam giác đều N.H1H2H3 với O là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm N thuộc trục Oz, ba nguyên tử hydrogen ở các vị trị H1,H2,H3 trong đó H1(0;−3;0) và H2H3 song song với trục Ox. Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen. (làm tròn kết quả đến hàng phần trăm)
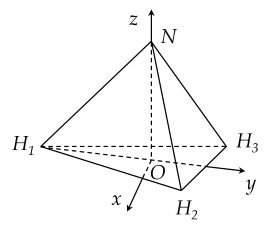
Trả lời:
Trong không gian, cho tứ diện ABCD có các điểm M,N,P lần lượt thuộc các cạnh BC,BD và AC sao cho BC=4BM;AC=3AP;BD=2BN. Mặt phẳng (MNP) cắt đường thẳng AD tại điểm Q. Tính tỉ số ADAQ. (kết quả viết dưới dạng số thập phân)
Trả lời:
Một giáo viên theo dõi sự tiến bộ của học sinh qua thang đo điểm, được mô hình hoá bằng hàm số f(x)=x3+ax2+bx+c với a,b,c là các hệ số. Trong đó, x(0≤x≤9,x∈N) là số tháng kể từ đầu năm học và f(x) là điểm trong tháng thứ x. Qua theo dõi, giáo viên ghi nhận tháng đầu tiên học sinh đạt 19 điểm, sau đó giảm trong tháng thứ hai và đến tháng thứ ba học sinh đạt mức điểm thấp nhất trong năm học, là 3 điểm. Kể từ tháng thứ ba trở đi, điểm của học sinh tăng lên. Tính điểm của học sinh đó ở tháng thứ sáu.
Trả lời:
Giả sử chi phí cho xuất bản x cuốn tạp chí (gồm: lương cán bộ, công nhân viên, giấy in,...) được cho bởi công thức:
C(x)=0,0001x2−0,2x+10000
trong đó C(x) được tính theo đơn vị là vạn đồng (1 vạn đồng =10000 đồng). Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số M(x)=xT(x) được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản x cuốn và tổng chỉ phí T(x) (xuất bản và phát hành) cho x cuốn tạp chí. Chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá 30000 cuốn?
Trả lời:
Một doanh nghiệp sản xuất độc quyền một loại sản phẩm. Giả sử khi sản xuất và bán hết x sản phẩm (0<x<2000), tổng số tiền doanh nghiệp thu được là F(x)=2000x−x2 (chục nghìn đồng) và tổng chi phí doanh nghiệp bỏ ra là G(x)=x2+1440x+50 (chục nghìn đồng). Công ty cũng phải chịu mức thuế phụ thu cho một đơn vị sản phẩm bán được là t (chục nghìn đồng), (0<x<300). Mức thuế phụ thu t (trên một đơn vị sản phẩm) là bao nhiêu nghìn đồng sao cho nhà nước thu được số tiền thuế phụ thu lớn nhất và doanh nghiệp cũng thu được lợi nhuận nhiều nhất theo đúng mức thuế phụ thu đó? (Kết quả làm tròn đến hàng đơn vị)
Trả lời:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau:
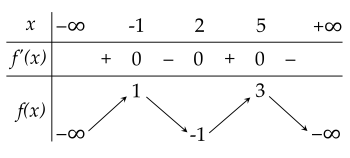
Phương trình f′[5−3f(x)]=0 có bao nhiêu nghiệm thực?
Trả lời:
