Đề kiểm tra chất lượng học kì II - PGD Hai Bà Trưng SVIP

Hướng dẫn giải:

1) Thay $x=1$ vào biểu thức: $A=\dfrac{\sqrt{1}+2}{\sqrt{1}-2}$
$A=-3$
2) Chứng minh $B=\dfrac{\sqrt{x}}{\sqrt{x}+2}$ với $x \geq 0, x \neq 4$.
$B=\dfrac{\sqrt{x}+2}{(\sqrt{x}-2)(\sqrt{x}+2)}+\dfrac{(\sqrt{x}+1)(\sqrt{x}-2)}{(\sqrt{x}+2)(\sqrt{x}-2)}-\dfrac{2 \sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}$
$=\dfrac{\sqrt{x}+2+x-\sqrt{x}-2-2 \sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}=\dfrac{x-2 \sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}$
$=\dfrac{\sqrt{x}(\sqrt{x}-2)}{(\sqrt{x}+2)(\sqrt{x}-2)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}$
3) Tìm $x$ để $A \cdot B \geq 0$
$A \cdot B=\dfrac{\sqrt{x}+2}{\sqrt{x}-2} \cdot \dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{\sqrt{x}}{\sqrt{x}-2}$.
TH1: $x=0 \Rightarrow \sqrt{x}=0 \Rightarrow A \cdot B=0$ (TM)
TH2: $x>0 \Rightarrow \sqrt{x}>0 \Rightarrow \sqrt{x}-2>0 \Rightarrow x>4$
Kết hợp điêu kiện: $x=0$ hoặc $x>4$ thỏa mãn yêu cầu.

Hướng dẫn giải:

Gọi vận tốc xe máy là $x(\mathrm{~km} /$ giờ $)(x>0)$
Thời gian xe máy đi hết quãng đường: $\frac{120}{x}$ (giờ)
Vận tốc ô tô: $x+20$ (km/giờ)
$\Rightarrow$ Thời gian ô tô đi hết quãng đường: $\frac{120}{x+20}$ (giờ)
Ô tô đến sớm hơn xe máy 1 giờ, ta có phương trình: $\frac{120}{x}-\frac{120}{x+20}=1$
Biến đổi đến phương trình: $x^{2}+20 x-2400=0$
Giải phương trình được: $x_{1}=40$ (TM) và $x_{2}=-60$ (loại).
Vậy vận tốc xe máy là $40 \mathrm{~km}$ /giờ, vận tốc ô tô là $60 \mathrm{~km}$ /giờ.

Hướng dẫn giải:

Bán kính đáy: $7: 2=3,5 \mathrm{~cm}$.
Thể tích sữa trong hộp: $\pi \times 3,5^{2} \times 8 \approx 3,14 \times 3,5^{2} \times 8$ $=307,72 \mathrm{~cm}^{3}=307,72 \mathrm{ml}$.

Hướng dẫn giải:

1) Tìm tọa độ giao điểm của (d) và (P) khi $m=2$
Thay $m=2$ vào $(d): y=2 x+3$
Xét phương trình hoành độ giao điểm : $x^{2}-2 x-3=0$
Giải phương trình tìm được $x_{1}=-1, x_{2}=3$
$\Rightarrow$ Tọa độ giao điểm $(-1 ; 1)$ và $(3 ; 9)$
2) Xét phương trình hoành độ giao điểm: $x^{2}-m x-3=0$ (1).
$\Delta=m^{2}+12 . m^{2} \geq 0 \Rightarrow \Delta=m^{2}+12 \geq 12>0 \text {. }$
Vậy phương trình luôn có 2 nghiệm phân biệt $\Rightarrow(d)$ cắt $(P)$ tại 2 điểm phân biệt
$x_{1}, x_{2}$ là 2 nghiệm của phương trình (1), theo hệ thức Vi - ét $\left\{\begin{array}{l}x_{1}+x_{2}=m \\ x_{1} x_{2}=-3\end{array}\right.$
$y_{1}=x_{1}^{2}, y_{2}=x_{2}^{2} \Rightarrow x_{1}^{2}+x_{2}^{2}=4\left(x_{1}+x_{2}\right)+3 \Leftrightarrow\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=4\left(x_{1}+x_{2}\right)+3$
$\Leftrightarrow m^{2}+6=4 m+3 \Leftrightarrow m^{2}-4 m+3=0 \Leftrightarrow\left[\begin{array}{l}m=1 \\ m=3\end{array}\right.$

Hướng dẫn giải:

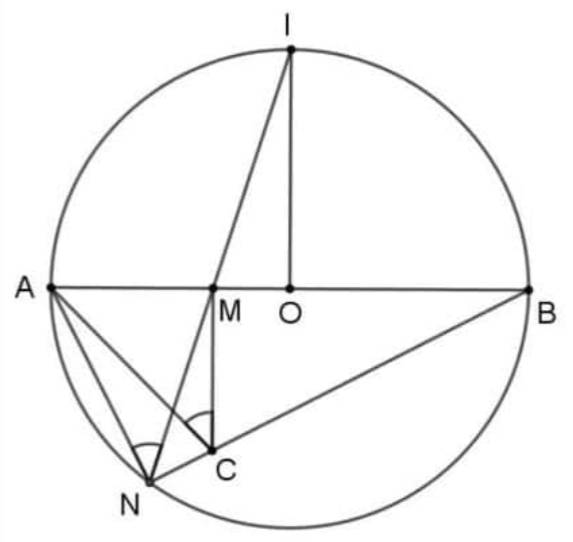
1) $\widehat{A M C}=90^{\circ} \Rightarrow A, M, C$ thuộc đường tròn đường kính $A C$
$\widehat{A N B}=90^{\circ} \Rightarrow \widehat{A N C}=90^{\circ} \Rightarrow A, N, C$ thuộc đường tròn đường kính $A C$ $\Rightarrow A, M, C, N$ cùng thuộc đường tròn đường kính $A C$.

2)Điểm $I$ chính giữa cung $A B \Rightarrow \mathrm{s} \overparen{A I}=90^{\circ}$
$\widehat{A N I}$ là góc nội tiếp chắn cung $A I \Rightarrow \widehat{A N I}=\frac{1}{2}$ sđ $\overparen{A I}$
$\Rightarrow \widehat{A N I}=45^{\circ} \Rightarrow \widehat{A N M}=45^{\circ}$
Chứng minh $A M=M C$
Tứ giác $A M C N$ nội tiếp $\Rightarrow \widehat{A C M}=\widehat{A N M}=45^{\circ}$ (cùng chắn cung $A M$ )
$\triangle A M C$ vuông tại $M, \widehat{A C M}=45^{\circ} \Rightarrow \triangle A C M$ vuông cân tại $M$
$\Rightarrow A M=M C$.

3) Chứng minh $\mathrm{MN}<R$
$M N=N I-I M$. NI là dây không qua tâm $\Rightarrow N I<2 R$
$I O \perp A B \Rightarrow I M>I O=R$ (M khác $O$, quan hệ đường xiên - đường vuông góc ) $\Rightarrow-I M<-R \Rightarrow M N=N I-I M<2 R-R=R$.

Hướng dẫn giải:

ĐKXĐ: $x \geq 1$
Xét vế trái: $(x-1)^{2} \geq 0 \Rightarrow \sqrt{(x-1)^{2}+1}+\sqrt{3(x-1)^{2}+4} \geq \sqrt{1}+\sqrt{4}=3$
Xét vế phải $\sqrt{x-1} \geq 0 \Rightarrow 3-\sqrt{x-1} \leq 3$
Vậy 2 vế cùng bằng $3$ khi $x=1$ (tmđk). Nghiệm của phương trình $x=1$