Tam giác cân. Đường trung trực của đoạn thẳng. SVIP

1. Tam giác cân và tính chất

a. Tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau.

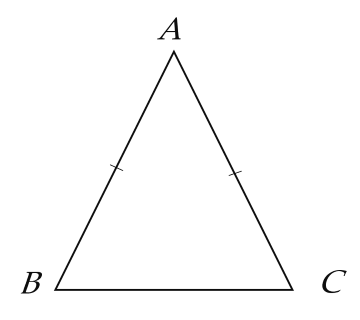
Trong hình trên, tam giác cân $ABC$ ($AB = AC$) được gọi là cân tại đỉnh $A$ , hai cạnh $AB$ và $AC$ là hai cạnh bên, $BC$ là cạnh đáy, $\widehat{B}$ và $\widehat{C}$ là hai góc ở đáy, $\widehat{A}$ là góc ở đỉnh. 

b. Tính chất của tam giác cân

Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Nhận xét: Tam giác $DEF$ có các cạnh bằng nhau và các góc bằng nhau. Đó là một tam giác đều.

Chú ý: Tam giác đều là tam giác có ba cạnh bằng nhau.

2. Đường trung trực của một đoạn thẳng

a. Đường trung trực của đoạn thẳng

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

Chú ý: Đường trung trực của một đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.

b. Tính chất của đường trung trực

Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

Ví dụ: Cho đoạn thẳng $AB$ và điểm $M$ không thuộc đoạn thẳng $AB$ sao cho $MA = MB$. Chứng minh rằng $M$ thuộc đường trung trực của $AB$.

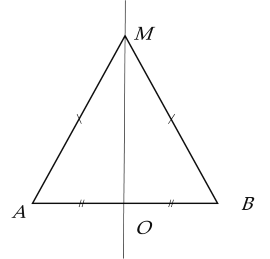
Giải

Gọi $O$ là trung điểm của đoạn thẳng $AB$.

Hai tam giác $OMA$ và $OMB$ có:

$OA = OB$ (do $O$ là trung điểm của đoạn thẳng $AB$)

$MA = MB$ (theo giả thiết)

$OM$ là cạnh chung.

Vậy $\Delta OMA = \Delta OMB$ (c.c.c). Suy ra $\widehat{AOM} = \widehat{BOM}$ (hai cạnh tương ứng).

Mặt khác, vì $\widehat{AOM} + \widehat{BOM} = 180^\circ$ nên $\widehat{AOM} = \widehat{BOM} = 90^\circ$. Vậy $MO$ vuông góc với $AB$, hay $MO$ là đường trung trực của đoạn thẳng $AB$.