

LÊ THỊ GIANG
Giới thiệu về bản thân



































Bạn Hà cần làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 1717 cm x 2525 cm, độ rộng viền xung quanh là xx (cm). Hỏi bạn Hà cần phải làm độ rộng viền khung ảnh tối đa bao nhiêu cm để diện tích của cả khung ảnh lớn nhất là 513513 (cm2).
a)
nΔ→=(3;4);nΔ1→=(5;−12).nΔ=(3;4);nΔ1=(5;−12).
cosα=∣cos(nΔ→;nΔ1→)∣=∣3.5+4.(−12)∣5.13=3365cosα=cos(nΔ;nΔ1)=5.13∣3.5+4.(−12)∣=6533.
b) (C)(C) có tâm I(3;−2)I(3;−2), bán kính R=6R=6
Đường thẳng dd có dạng 4x−3y+m=04x−3y+m=0 (mm khác 77)
dd tiếp xúc (C)(C) khi và chỉ khi d(I,d)=R⇔∣12+6+m∣5=6d(I,d)=R⇔5∣12+6+m∣=6.
Tìm được m=−48m=−48(TM), m=12m=12 (TM)
Vậy có hai đường thẳng dd thỏa mãn là 4x−3y−48=04x−3y−48=0 và 4x−3y+12=04x−3y+12=0.
a) Ta có f(x)=x2+2(m−1)x+m+5f(x)=x2+2(m−1)x+m+5 có Δ′=(m−1)2−(m+5)=m2−3m−4Δ′=(m−1)2−(m+5)=m2−3m−4
Lại có hệ số a=1>0a=1>0.
Để f(x)f(x) luôn dương (cùng dấu hệ số aa) với mọi x∈Rx∈R thì Δ′<0Δ′<0 ⇔m2−3m−4<0⇔m2−3m−4<0.
Xét tam thức h(m)=m2−3m−4h(m)=m2−3m−4 có Δm=9−4.(−4)=25>0Δm=9−4.(−4)=25>0 nên h(m)h(m) có hai nghiệm là m1=−1m1=−1 và m2=4m2=4.
Ta có bảng xét dấu của h(m)h(m):
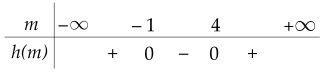
Do đó h(m)<0h(m)<0 với mọi x∈(−1;4)x∈(−1;4)
Hay Δ′<0Δ′<0 với mọi x∈(−1;4)x∈(−1;4)
Vậy x∈(−1;4)x∈(−1;4) thì tam thức bậc hai f(x)=x2+(m−1)x+m+5f(x)=x2+(m−1)x+m+5 dương với mọi x∈Rx∈R.
b) Bình phương hai vế ta được: 2x2−8x+4=x2−4x+42x2−8x+4=x2−4x+4
⇔x2−4x=0⇔x2−4x=0
Suy ra x=0x=0 hoặc x=4x=4
Thử lại nghiệm được x=4x=4 thỏa mãn phương trình.
Vậy tập nghiệm S=4S=4.
Ta có: dd // Δ:x+4y−2=0⇒Δ:x+4y−2=0⇒ Phương trình dd có dạng: x+4y+c=0x+4y+c=0.
Mặt khác: d(A,d)=3⇒∣−2+4.3+c∣1+16=3⇒∣10+c∣=317d(A,d)=3⇒1+16∣−2+4.3+c∣=3⇒∣10+c∣=317
⇒[c=317−10 c=−317−10⇒[d1:x+4y+317−10=0d2:x+4y−317−10=0 ⇒[c=317−10 c=−317−10⇒[d1:x+4y+317−10=0d2:x+4y−317−10=0
Vậy có hai đường thẳng thỏa mãn: x+4y+317−10=0x+4y+317−10=0; x+4y−317−10=0x+4y−317−10=0.
a) Gọi C(xC;yC)C(xC;yC).
Ta có: OC→=(xC;yC)OC=(xC;yC), AB→=(−2;5)⇒−3AB→=(6;−15)AB=(−2;5)⇒−3AB=(6;−15);
OC→=−3AB→⇔{xC=6yC=−15⇒C(6;−15)OC=−3AB⇔{xC=6yC=−15⇒C(6;−15)
b) DD đối xứng với AA qua CC hay CC là trung điểm của AD⇔{xC=xA+xD2yC=yA+yD2AD⇔⎩⎨⎧xC=2xA+xDyC=2yA+yD
⇔{xD=2xC−xA=2.6−3=9yD=2yC−yA=2(−15)−(−5)=−25 ⇔⎩⎨⎧ xD=2xC−xA=2.6−3=9yD=2yC−yA=2(−15)−(−5)=−25
⇒D(9;−25)⇒D(9;−25).
Bình phương hai vế phương trình, ta được: 2x2+5=x2−x+11⇔x2+x−6=0⇔x=22x2+5=x2−x+11⇔x2+x−6=0⇔x=2 hoặc x=−3x=−3.
Thay giá trị x=2x=2 vào phương trình: 13=1313=13 (thỏa mãn).
Thay giá trị x=−3x=−3 vào phương trình: 23=2323=23 (thỏa mãn).
Vậy tập nghiệm phương trình là S={2;−3}S={2;−3}.
Khi bán hết xx sản phẩm thì số tiền thu được là: 170x170x (nghìn đồng).
Điều kiện để nhà sản xuất không bị lỗ là 170x≥x2+30x+3300⇔x2−140x+3300≤0170x≥x2+30x+3300⇔x2−140x+3300≤0.
Xét x2−140x+3300=0⇒x=30x2−140x+3300=0⇒x=30 hoặc x=110x=110.
Bảng xét dấu f(x)=x2−140x+3300f(x)=x2−140x+3300:
∞!aaaaa + ∞ − + ∞ − xf(x)00 + 30110
Ta có: x2−140x+3300≤0⇔x∈[30;110]x2−140x+3300≤0⇔x∈[30;110].
Vậy nếu nhà sản xuất làm ra từ 3030 đến 110110 sản phẩm thì họ sẽ không bị lỗ.