

Lương Bảo Phương
Giới thiệu về bản thân



































a) \(2,5\times3,4\times4\)
\(=2,5\times4\times3,4\)
\(=\left(2,5\times4\right)\times3,4\)
\(=10\times3,4\)
\(=34\)
b) \(2\times5,6\times0,5\)
\(=2\times0,5\times5,6\)
\(=\left(2\times0,5\right)\times5,6\)
\(=1\times5,6\)
\(=5,6\)
c) \(0,5\times45\times2000\)
\(=0,5\times2000\times45\)
\(=\left(0,5\times2000\right)\times45\)
\(=1000\times45\)
\(=45000\)
d) \(0,27\times5,2+0,27\times4,8\)
\(=0,27\times\left(5,2+4,8\right)\)
\(=0,27\times10\)
\(=2,7\)
e) \(25,7+9,48+14,3\)
\(=25,7+14,3+9,48\)
\(=\left(25,7+14,3\right)+9,48\)
\(=40+9,48\)
\(=49,48\)
g) \(34,6+22,5+15,4\)
\(=34,6+15,4+22,5\)
\(=\left(34,6+15,4\right)+22,5\)
\(=50+22,5\)
\(=72,5\)
\(66\times10=660\)
II write the correct form of the words in brackets
1.a trip to fansipan is an (forget) unforgettabe experience
2.you can watch(tradition) traditions lances when you visit sa pa
3.many people think that the greatest(attract) attraction in hue is the temples
4.you must take an umbrella because it's(rain) rainy in mui ne at this time of the year
5.The perfume river is the most(fame) famous river in central viet nam
#Tiếng anh lớp 6Đáy lớn thửa ruộng hình thang là:
\(18\times\dfrac{4}{3}=24\left(m\right)\)
Diện tích thửa ruộng hình thang là:
\(\dfrac{\left(24+18\right)\times12}{2}=252\left(m^2\right)\)
Số thóc có trên thửa ruộng hình thang là:
\(252\div100\times60=151,2\left(kg\right)\)
Đáp số: \(151,2\) \(kg\) thóc\(.\)
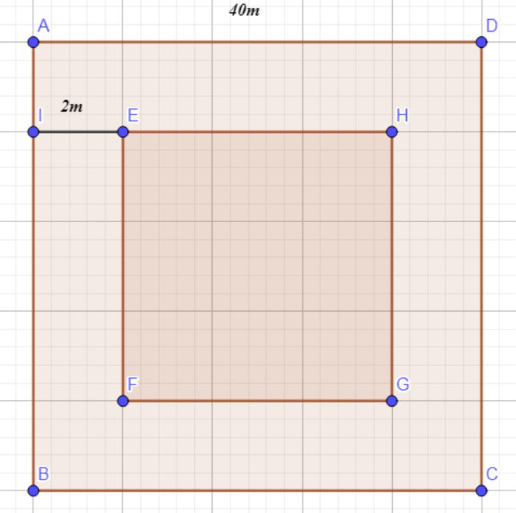
a) Độ dài 1 cạnh phần trồng rau cải xanh là:
\(40-\left(2+2\right)=36\left(m\right)\)
Diện tích phần trồng rau là:
\(36\cdot36=1296\left(m^2\right)\)
Số ki \(-\) lô \(-\) gam rau mà bác Lâm thu hoạch được là:
\(1296\cdot2=2592\left(kg\right)\)
Số tiền mà bác Lâm thu được là:
\(20000\cdot2592=51840000\) (đồng)
b) Diện tích mảnh vườn đó là:
\(40\cdot40=1600\left(m^2\right)\)
Diện tích lối đi xung quanh vườn là:
\(1600-1296=304\left(m^2\right)\)
Đáp số: a) \(51840000\) đồng
b) \(304m^2\)
Chiều dài vườn hoa là:
\(18,5\times5=92,5\left(m\right)\)
Chu vi vườn hoa là:
\(\left(18,5+92,5\right)\times2=222\left(m\right)\)
Diện tích vườn hoa là:
\(18,5\times92,5=1711,25\left(m^2\right)\)
Đáp số: Chu vi: \(222m\)
Diện tích: \(1711,25m^2\)
Tôi là áo 4 chân 1 lưng nhưng không có cơ thể. Tôi là cái gì?
Đáp án: Cái bàn