a) Xét ΔABD vuông tại A và ΔHBD vuông tại H có:
- BD là cạnh chung

- \(\widehat{ABD}=\widehat{HBD}\) (vì BD là tia phân giác \(\widehat{ABC}\))

Suy ra ΔABD = ΔHBD (cạnh huyền - góc nhọn)

b) Từ a) suy ra AD = DH (hai cạnh tương ứng)

c) Đề bị thiếu: Điểm M ở đâu???

Xét hiệu \(x-y=\dfrac{m}{m}-\dfrac{m^2}{n^2}=\dfrac{mn^2-m^3}{mn^2}\)

Mà m > n nên \(mn^2< m^3\), suy ra x - y < 0 hay x < y

Ta có \(M=\dfrac{2n+1}{n-1}\) xác định khi n - 1 ≠ 0 hay n ≠ 1

Vì n ϵ Z nên 2n + 1 ϵ Z và n - 1 ϵ Z, suy ra M ϵ Q

Vậy n ϵ {Z | n ≠ 1}

Đề thiếu: không trả lời câu hỏi thì có thay đổi điểm hay không?

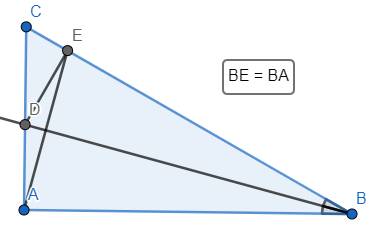
a) Xét ΔABD và ΔEBD có:

- BE = BA (giả thuyết)

- \(\widehat{ABD}=\widehat{EBD}\) (vì BD là tia phân giác của \(\widehat{ABC}\) )

- BD là cạnh chung

Suy ra ΔABD = ΔEBD (c.g.c)

b) Từ a) suy ra DE = AD (vì hai cạnh tương ứng) và \(\widehat{BAD}=\widehat{BED}=90^o\) (vì hai góc tương ứng), hay \(DE\perp BC\)

c) Từ BE = BA và DE = AD suy ra B và D đều nằm trên đường trung trực của AE, hay BD là đường trung trực của AE

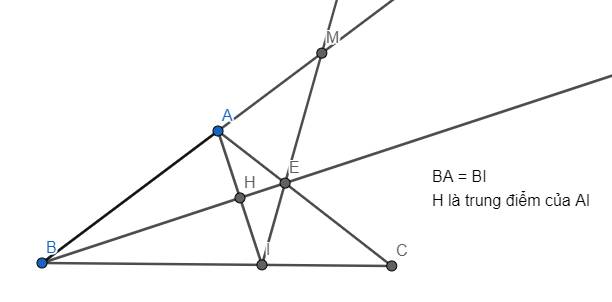
a) Xét ΔABI có:

- BA = BI, suy ra ΔABI cân tại B

- BH là đường trung tuyến đáy AI của ΔABI (do H là trung điểm của AI)

Suy ra BH cũng là đường cao, cũng là đường trung trực của ΔABI.

Khi đó ΔABH & ΔIBH đều vuông tại H. Hai tam giác này có BH là cạnh chung và BA = BI (giả thuyết) nên ΔABH = ΔIBH (cạnh huyền - cạnh góc vuông).

b) Vì BH là đường trung trực của ΔABI (chứng minh trên) và E thuộc BH nên EA = EI. Suy ra ΔAEI cân.

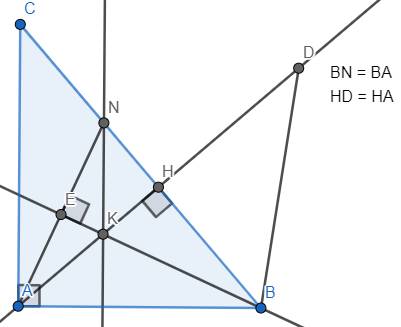
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:

- BE là cạnh chung, BN = BA (giả thuyết)

Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)

b) Theo đề ta có BH vuông góc với AD và HA = HD

Suy ra BH là đường trung trực của AD

Suy ra BA = BD (vì B nằm trên đường trung trực của AD)

c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K

Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB

Mà AC cũng vuông góc với AB, suy ra NK // CA

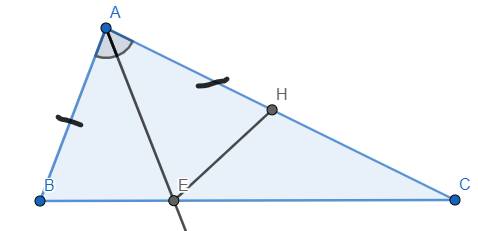
a) Xét ΔABE & ΔAHE có:

- AB = AH (giả thuyết); AE là cạnh chung; \(\widehat{BAE}=\widehat{HAE}\) (vì AE là tia phân giác góc BAC)

Suy ra ΔABE = ΔAHE (c.g.c)

a) Ta có:

A(x) + B(x) = (2x³ - x² + 3x - 5) + (2x³ + x² + x + 5)

                  = 4x³ + 4x

b) Ta có H(x) = A(x) + B(x) = 4x³ + 4x = 0

                                      => 4x(x² + 1) = 0

                                      => 4x = 0 hoặc x² + 1 = 0

                                      => x = 0 : 4 = 0 hoặc x² = 0 - 1 = -1 (vô lí)

Vậy nghiệm của H(x) = A(x) + B(x) là x = 0

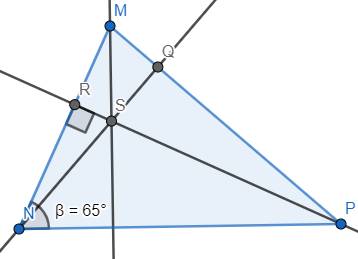
a) Theo đề ta có S là trực tâm của tam giác MNP và MNP là tam giác nhọn

Suy ra MS cũng là đường cao đáy NP, hay \(MS\perp NP\)

b) Gọi O là giao điểm của MS và NP. Ta có MNO là tam giác vuông tại O

Suy ra \(\widehat{MNO}+\widehat{NMO}=90^o\) hay \(\widehat{MNP}+\widehat{SMR}=90^o\)

Suy ra \(\widehat{SMR}=90^o-\widehat{MNP}=90^o-65^o=25^o\)