\(6\times\left(15+5x\right)=300\)

\(15+5x=300:6\)

\(15+5x=50\)

\(5x=50-15\)

\(5x=35\)

\(x=7\)

Vườn không nhà trống

Mik đoán là vậy

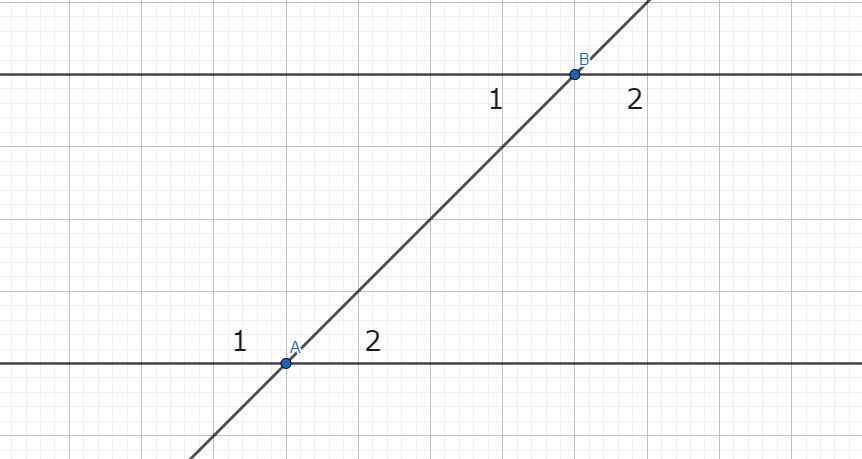 Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)

Mặt khác:

\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\) (hai cặp góc kề bù)

Mà \(\widehat{A_1}=\widehat{B_2}\) nên:

\(\widehat{A_2}=\widehat{B_1}\) Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các cặp góc so le trong còn lại cũng bằng nhau.

Kho thứ ba có số thóc là:

\(765:\left(2+7\right)\times2=170\) (tấn)

Tổng số thóc của kho thứ nhất và kho thứ hai là:

\(765-170=595\) (tấn)

Kho thứ nhất có số thóc là:

\(\left(595-95\right):2=250\) (tấn)

Kho thứ hai có số thóc là:

\(250+95=345\) (tấn)

Đáp số:...

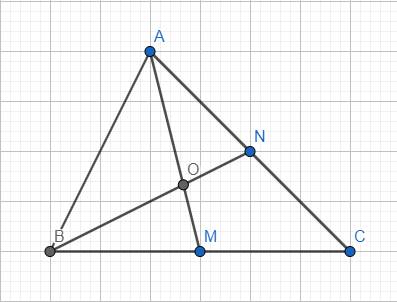
\(\text{△ABC}\) có: \(AM,BN\) là 2 đường trung tuyến (gt)

Mà \(O\) là giao điểm của \(AM\) và \(BN\) nên:

\(O\) là trọng tâm của \(\text{△ABC}\)

\(\Rightarrow ON=\dfrac{1}{2}OB\) (theo tính chất ba đường trung tuyến trong tam giác)

Thay \(ON=1\) được:

\(OB=2\cdot ON=2\cdot1=2\)

Vậy \(OB=2\)

Gọi phân số đó là \(x\)

Ta có:

\(\left(x-\dfrac{5}{4}\right):3+\dfrac{1}{4}=2\)

\(\left(x-\dfrac{5}{4}\right):3=2-\dfrac{1}{4}\)

\(\left(x-\dfrac{5}{4}\right):3=\dfrac{7}{4}\)

\(x-\dfrac{5}{4}=\dfrac{7}{4}\times3\)

\(x-\dfrac{5}{4}=\dfrac{21}{4}\)

\(x=\dfrac{21}{4}+\dfrac{5}{4}\)

\(x=\dfrac{26}{4}=\dfrac{13}{2}\)

Vậy...

Quy luật: Lấy tổng 2 số ở trên nhân cho tích 2 số ở dưới được số cần tìm

Số cần tìm là: \(\left(4+5\right)\times\left(7\times6\right)=9\times42=378\)

\(\left(\dfrac{3}{4}+x\right)\times50\%=3,4\)

\(\dfrac{3}{4}+x=3,4:50\%\)

\(\dfrac{3}{4}+x=6,8\)

\(x=6,8-\dfrac{3}{4}\)

\(x=6,05\)

A

a)\(A=-1,2ab^4-5a^2b^2+3-1,2ab^4-6a^2b^2-\dfrac{2}{3}ab-3\)

\(A=\left(-1,2ab^4-1,2ab^4\right)+\left(-5a^2b^2-6a^2b^2\right)-\dfrac{2}{3}ab+\left(3-3\right)\)

\(A=-2,4ab^4-11a^2b^2-\dfrac{2}{3}ab\)

Vậy...

b)Ta có: \(a=-2;b=\left(-2025\right)^0=1\)

Thay \(a=-2;b=\left(-2025\right)^0=1\) vào A được:

\(A=-2,4.\left(-2\right).1-11.\left(-2\right)^2.1^2-\dfrac{2}{3}.\left(-2\right).1\)

\(A=4,8-44+\dfrac{4}{3}\)

\(A=-\dfrac{568}{15}\)

Vậy...