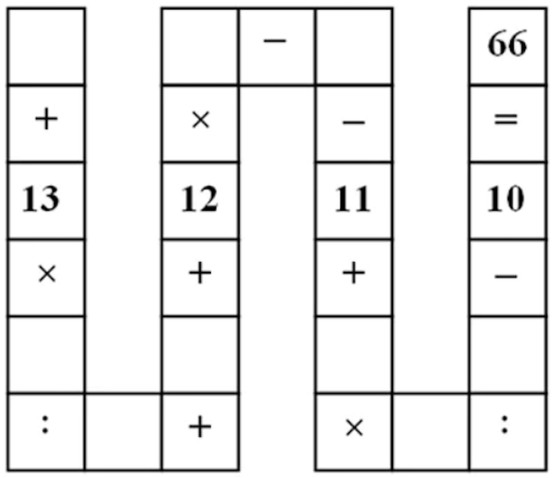
The points M, N, P on the sides BC, CA, AB, respectively, are such that the triangle MNP is acute. Let \(x\) be the length og the shortest altitude in the triangle ABC and let \(X\) be the length of the largest altitude in the triangle MNP. Prove that \(x\le2X\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

\(D=ℝ\)
Có \(y'=x^2-2x-m\)
Xét \(y'=0\)
\(\Leftrightarrow x^2-2x-m=0\)
\(\Leftrightarrow m=x^2-2x\) (1)
YCBT \(\Leftrightarrow\) (1) có 2 nghiệm phân biệt thuộc \(\left(3;4\right)\)
Đặt \(f\left(x\right)=x^2-2x\). Khi đó \(f'\left(x\right)=2x-2\)
\(f'\left(x\right)=0\Leftrightarrow x=1\)
Lập BBT, ta thấy để \(m=f\left(x\right)\) có 2 nghiệm phân biệt thuộc \(\left(3;4\right)\) thì \(3< m< 8\)
Khi đó \(m\in\left\{4;5;6;7\right\}\), suy ra có 4 giá trị nguyên của m thỏa mãn ycbt.
-> Chọn B.

Chọn `D.` Thế năng cực đại tại vị trí vận tốc đổi chiều.
- Vì:
Khi vận tốc của vật đổi chiều thì lúc đó vật đang ở vị trí biên dương (hoặc biên âm) `=>x=+-A`.
Mà `W_t =1/2 kx^2`
`=>W_t=1/2 kA^2 =W_[t(max)]`

#include <bits/stdc++.h>
using namespace std;
int main()
{
int n,A[100],i,kt,j;
cin>>n;
for (int i=1; i<=n; i++)
cin>>A[i];
for (int i=1; i<=n; i++)
if (A[i]>1)
{
kt=0;
for (int j=2; j*j<=A[i]; j++)
if (A[i]%j==0) kt=1;
if (kt==0) cout<<A[i]<<" ";
}
return 0;
}

b) Xét pt hoành độ giao điểm của hàm số đã cho và Ox là \(2x^3+2\left(6m-1\right)x^2-3\left(2m-1\right)x-3\left(1+2m\right)=0\) (*)
Ta thấy \(x=1\) là nghiệm của pt trên. Lập sơ đồ Horner:
| \(2\) | \(2\left(6m-1\right)\) | \(-3\left(2m-1\right)\) | \(-3\left(1+2m\right)\) | |
| \(x=1\) | \(2\) | \(12m\) | \(6m+3\) | \(0\) |
Do đó pt (*)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+12mx+6m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2x^2+12mx+6m+3=0\end{matrix}\right.\)
Xét pt \(2x^2+12mx+6m+3=0\) (1)
Ycbt \(\Leftrightarrow\) pt (1) có 2 nghiệm phân biệt \(x_1,x_2\) khác 1 và thỏa mãn \(x_1^2+x_2^2=27\)
Có \(\Delta'=\left(6m\right)^2-2\left(6m+3\right)=36m^2-12m-6>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{1+\sqrt{7}}{6}\\m< \dfrac{1-\sqrt{7}}{6}\end{matrix}\right.\)
Có 2 nghiệm khác 1 \(\Leftrightarrow2.1^2+12m.1+6m+3\ne0\)
\(\Leftrightarrow18m+5\ne0\)
\(\Leftrightarrow m\ne-\dfrac{5}{18}\)
Theo định lý Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-6m\\x_1x_2=\dfrac{6m+3}{2}\end{matrix}\right.\)
Để \(x_1^2+x_2^2=27\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=27\)
\(\Leftrightarrow\left(-6m\right)^2-2.\dfrac{6m+3}{2}=27\)
\(\Leftrightarrow36m^2-6m-3=27\)
\(\Leftrightarrow6m^2-m-5=0\)
\(\Leftrightarrow6m^2-6m+5m-5=0\)
\(\Leftrightarrow6m\left(m-1\right)+5\left(m-1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(6m+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(nhận\right)\\m=-\dfrac{5}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy \(m=1\) hoặc \(m=-\dfrac{5}{6}\) thỏa ycbt.
c) Xét pt \(x^3-3mx^2+\left(3m-1\right)x+6m=0\) (*)
Ta thấy (*) có nghiệm \(x=-1\). Lập sơ đồ Horner:
| \(1\) | \(-3m\) | \(3m-1\) | \(6m\) | |
| \(x=-1\) | \(1\) | \(-3m-1\) | \(6m\) | \(0\) |
Vậy (*) \(\Leftrightarrow\left(x+1\right)\left(x^2-\left(3m+1\right)x+6m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2-\left(3m+1\right)x+6m=0\end{matrix}\right.\)
Tới đây thì làm tương tự câu b) nhé.

a) Gọi K' là giao điểm của BI và EF, S là giao điểm của EJ và AB.
Ta có \(\left(FSBA\right)=-1\) (hàng điều hòa quen thuộc). Mặt khác, dễ thấy K'B là trung trực của FJ nên K'B cũng là tia phân giác của \(\widehat{FK'S}\)
Do đó, \(\widehat{AK'B}=90^o\). Khi đó tam giác AK'B vuông tại K' có trung tuyến K'M nên \(K'M=MB=\dfrac{1}{2}AB\)
Từ đó suy ra tam giác MK'B cân tại M \(\Rightarrow\widehat{MK'B}=\widehat{MBK'}=\widehat{K'BC}\)
Do đó MK'//BC. Chú ý rằng MN là đường trung bình của tam giác ABC \(\Rightarrow\) MN//BC. Vậy \(K'\in MN\) hay K' chính là giao điểm của MN và JE. Điều này có nghĩa là \(K'\equiv K\).
Như vậy, \(K,B,I\) thẳng hàng và \(\widehat{AKB}=90^o\) hay \(AK\perp BI\)
Lại có \(FJ\perp BI\) nên AK//FJ hay AK//HJ.
Tương tự, ta cũng có AH//KJ nên tứ giác AKJH là hình bình hành.
\(\Rightarrow\) HK, AJ cắt nhau tại trung điểm mỗi đoạn, hay JA đi qua trung điểm của HK.
câu a ý 2:
Gọi U là giao điểm của EF và BC, P là trung điểm BC, X là điểm chính giữa cung BC không chứa D của (O).
Có \(\widehat{XIB}=\widehat{IAB}+\widehat{IBA}=\widehat{XCB}+\widehat{IBC}=\widehat{XBC}+\widehat{IBC}=\widehat{XBI}\) nên tam giác XBI cân tại X \(\Rightarrow XB=XI\)
Tương tự, ta cũng có \(XB=XC=XI\) nên X là tâm (IBC)
Dễ thấy \(\widehat{XBD}=\widehat{XCD}=90^o\) nên XB, XC là tiếp tuyến tại B và C của (X).
\(\Rightarrow DC^2=DP.DX=DT.DG\) \(\Rightarrow\) Tứ giác TPXG nội tiếp.
\(\Rightarrow\widehat{DPT}=\widehat{XGT}=\widehat{XTG}=\widehat{XPG}\)
\(\Rightarrow90^o-\widehat{DPT}=90^o-\widehat{XPG}\)
\(\Rightarrow\widehat{UPT}=\widehat{UPG}\) . Do \(\widehat{UPG}+\widehat{GPC}=180^o\)
\(\Rightarrow\) \(\widehat{GPC}+\widehat{UPT}=180^o\)
Vì D là giao điểm của 2 tiếp tuyến tại B và C của đường tròn (X) nên GD là đối trung của tam giác GBC
\(\Rightarrow\widehat{BGT}=\widehat{PGC}\)
Lại có \(\widehat{GTB}=\widehat{GCP}\) \(\Rightarrow\Delta GTB\sim\Delta GCP\) \(\Rightarrow\widehat{GBT}=\widehat{GPC}\)
Lại có \(\widehat{GBT}=\widehat{GIT}\) nên \(\widehat{GPC}=\widehat{GIT}\)
Kết hợp với \(\widehat{GPC}+\widehat{UPT}=180^o\), ta có \(\widehat{GIT}+\widehat{UPT}=180^o\)
\(\Rightarrow\) Tứ giác ITPJ nội tiếp.
Mặt khác, \(\left(BCJU\right)=-1\) và P là trung điểm BC nên \(\overline{UJ}.\overline{UP}=\overline{UB}.\overline{UC}\) (hệ thức Maclaurin)
\(\Rightarrow P_{U/\left(ITPJ\right)}=P_{U/\left(X\right)}\)
\(\Rightarrow\) U nằm trên trục đẳng phương của đường tròn (ITPJ) và (X), mà IT là trục đẳng phương của 2 đường tròn này nên U, I, T thẳng hàng.
Xét cực và đối cực đối với (I). Kí hiệu \(d_Y\) là đối cực của Y đối với (I).
Ta có \(\left(BCJU\right)=-1\) \(\Rightarrow J\in d_U\)
Lại có \(U\in EF\equiv d_A\Rightarrow A\in d_U\)
Do đó \(JA\equiv d_U\) \(\Rightarrow JA\perp UI\) hay \(JA\perp IT\) (đpcm)