x(y-3)=10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
\(\left(-\dfrac{2}{3}\right)^3=\dfrac{\left(-2\right)^3}{3^3}=-\dfrac{8}{27}\)
\(\left(-1\dfrac{3}{4}\right)^2=\left(-\dfrac{7}{4}\right)^2=\dfrac{\left(-7\right)^2}{4^2}=\dfrac{49}{16}\)
\(\left(-0,1\right)^4=\left(\left(-0,1\right)^2\right)^2=\left(0,01\right)^2=0,0001\)
\(\left(-\dfrac{2}{3}\right)^{2022}:\left(-\dfrac{2}{3}\right)^{2019}=\left(-\dfrac{2}{3}\right)^3=\dfrac{\left(-2\right)^3}{3^3}=-\dfrac{8}{27}\)
Bài 2.
a) \(\left(-\dfrac{1}{3}\right)^2.\left(-\dfrac{1}{3}\right)=\left(-\dfrac{1}{3}\right)^3=\dfrac{\left(-1\right)^3}{3^3}=-\dfrac{1}{27}\)
b) \(\left(-2\right)^2.\left(-2\right)^3=\left(-2\right)^5=-32\)
c) \(a^5.a^7=a^{12}\)
Bài 3.
a) \(x^2=\dfrac{4}{9}\Leftrightarrow x=\pm\dfrac{2}{3}\)
b) \(x^3=\dfrac{8}{27}\Leftrightarrow x=\dfrac{2}{3}\)
c) \(x^3=-\dfrac{8}{125}\Leftrightarrow x=-\dfrac{2}{5}\)

Giả sử hai phân số cần tìm là \(\dfrac{a}{7}\)và \(\dfrac{b}{7}\)
Theo bài ra ta có: \(\dfrac{-3}{8}< \dfrac{a}{7}< \dfrac{b}{7}< \dfrac{-1}{8}\)
Hay \(\dfrac{-21}{56}< \dfrac{8a}{56}< \dfrac{8b}{56}< \dfrac{-7}{56}\)
\(\Leftrightarrow-21< 8a< 8b< -7\)
Vì a,b là các số nguyên nên dễ thấy a = -2 và b = -1 thõa mãn đầu kiện bài toán.
Vậy hai phân số cần tìm là: -2/7 và -1/7

Cộng đa thức thì cứ cộng đơn thức lại với nhau. Bạn viết như đề không biết chỗ nào là mũ, chỗ nào là hệ số

Ta có:
\(3x+5\ge0\Rightarrow x\ge\dfrac{-5}{3}\)
\(6+x\ge0\Rightarrow x\ge-6\)
a. TH1: \(x\le-6\)
PT đã cho có dạng: \(-3x-5-6-x=2\Leftrightarrow-4x=13\Rightarrow x=\dfrac{-13}{4}>-6\) loại.
TH2: \(-6< x< \dfrac{-5}{3}\)
Ta có: \(-3x-5+6+x=2\Leftrightarrow-2x=1\Rightarrow x=\dfrac{-1}{2}\)Loại
TH3: \(x\ge\dfrac{-5}{3}\)
Ta có: \(3x+5+6+x=2\Leftrightarrow4x=-9\Rightarrow x=\dfrac{-9}{4}< \dfrac{-5}{3}\) loại.
Vậy phương trình đã cho vô nghiệm.
B. xét các trường hợp tương tự câu a ta cũng kết luận phương trình vô nghiệm

Đề không đủ dữ kiện để giải. Trong trường hợp này x,y là số nguyên có thể giải ra nghiệm chứ hữu tỉ thì vô số rồi

\(s=\dfrac{1}{2022}\left(\dfrac{2}{1}+\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}+...+\dfrac{2023}{2022}\right)\)
\(=\dfrac{1}{2022}\left(1+\dfrac{1}{1}+1+\dfrac{1}{2}+1+\dfrac{1}{3}+1+\dfrac{1}{4}+1+\dfrac{1}{5}+...+1+\dfrac{1}{2022}\right)\)
\(=\dfrac{1}{2022}\left(2022+1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{2022}\right)\)
\(=1+\dfrac{1}{2022}\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{2022}\right)\)
Ta có:
\(=1< 1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{2022}< 2022\)
Nên \(0< \dfrac{1}{2022}\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{2022}\right)< 1\)
Suy ra:
\(1< 1+\dfrac{1}{2022}\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{2022}\right)< 2\)
Hay \(1< S< 2\)
Dễ thấy S không phải là số tự nhiên (đpcm)
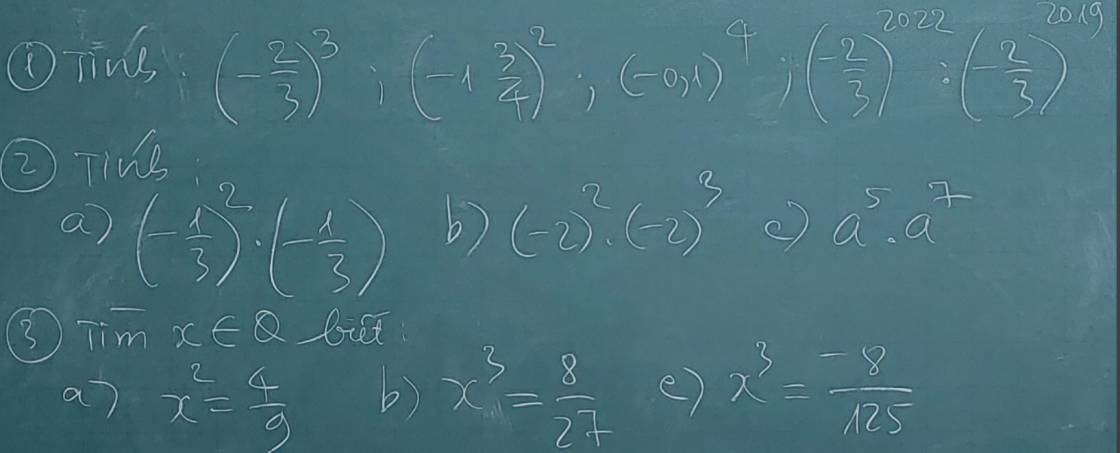
x(y-3) = 10
⇔ x(y-3) = 2.5
⇔ x = 2 và y - 3 = 5 ⇔ x =2; y = 8
hoặc x = 5 và y - 3 = 2 ⇔ x = 5; y = 5
vậy các cặp x,y nguyên thỏa mãn đề bài là:
(2;8) và (5;5)
Đề bài yêu cầu gì vậy em?