Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi x là số mét vải loại II mua được (x > 0, mét)
Số mét vải mỗi loại mua được tỉ lệ nghịch với giá tiền một mét vải là :
60/x = 120/100
Nên x = 50
Vậy số mét vải loại II mua được là 50 m

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=\dfrac{\left(bd\right)\cdot k^2}{bd}=k^2\left(1\right)\)
\(VP=\dfrac{2009a^2+2010c^2}{2009b^2+2010d^2}=\dfrac{2009\cdot\left(bk\right)^2+2010\cdot\left(dk\right)^2}{2009b^2+2010d^2}\\ =\dfrac{2009b^2\cdot k^2+2010d^2\cdot k^2}{2009b^2+2010d^2}=\dfrac{k^2\cdot\left(2009b^2+2010d^2\right)}{2009b^2+2010d^2}\\ =k^2\left(2\right)\)
Từ (1) và (2) => \(\dfrac{ac}{bd}=\dfrac{2009a^2+2010c^2}{2009b^2+2010d^2}\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{a^2+ac}{c^2-ac}=\dfrac{\left(bk^2\right)+bk\cdot dk}{\left(dk\right)^2-bk\cdot dk}\\ =\dfrac{b^2k^2+bdk^2}{d^2k^2-bdk^2}=\dfrac{k^2\left(b^2+bd\right)}{k^2\left(d^2-bd\right)}=\dfrac{b^2+bd}{d^2+bd}=VP\)

\(\dfrac{a}{b}=\dfrac{b}{d}=>b^2=ad\)
Ta có:
\(VT=\dfrac{a^2+b^2}{b^2+d^2}=\dfrac{a^2+ad}{ad+d^2}=\dfrac{a\left(a+d\right)}{d\left(a+d\right)}=\dfrac{a}{d}=VP\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{5a+3b}{5a-3b}=\dfrac{5bk+3b}{5bk-3b}=\dfrac{b\left(5k+3\right)}{b\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\\ =\dfrac{d\left(5k+3\right)}{d\left(5k-3\right)}=\dfrac{5dk+3d}{5dk-3d}=\dfrac{5c+3d}{5c-3d}=VP\)

\(\dfrac{2}{15}-\dfrac{7}{10}\\ =\dfrac{4}{30}-\dfrac{21}{30}\\ =\dfrac{4-21}{30}\\ =\dfrac{-17}{30}\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\b=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}\\ =\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(1\right)\)
\(VP=\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=\dfrac{bd\cdot k^2}{bd}=k^2\left(2\right)\)
Từ (1) và (2) => \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{ac}{bd}\)
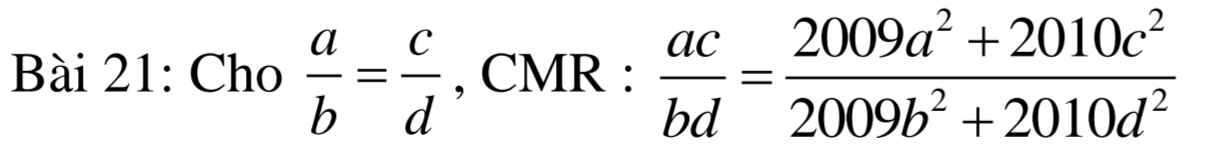
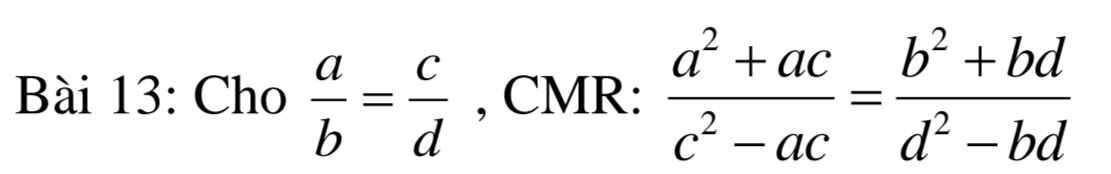
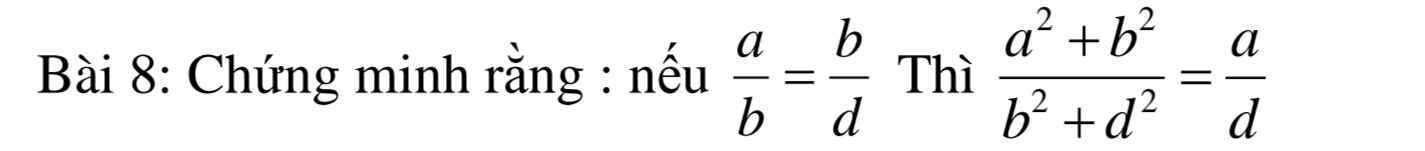

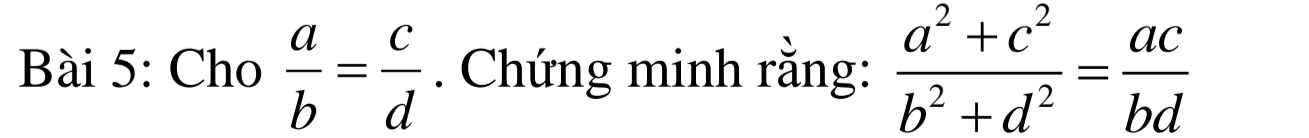
Bài 1:
Số lần bắn được ít nhất 8 điểm là:
5+6+5=16(lần)
=>Xác suất để bắn được ít nhất 8 điểm là \(P=\dfrac{16}{20}=\dfrac{4}{5}\)
Bài 2:
a: Xác suất xuất hiện mặt N là: \(\dfrac{18}{22}=\dfrac{9}{11}\)
b: Số lần xuất hiện mặt S là 25-11=14(lần)
Xác suất xuất hiện mặt S là \(\dfrac{14}{25}\)
c: Xác suất xuất hiện mặt N là \(\dfrac{14}{30}=\dfrac{7}{15}\)