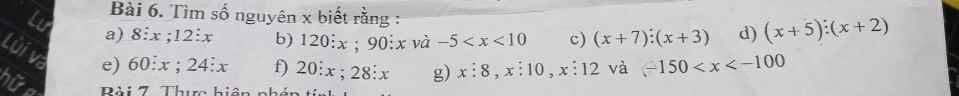a, 8\(⋮\) \(x\); 12 \(⋮\) \(x\)

⇒ \(x\) \(\in\) ƯC(8; 12)

    8 = 2³; 12 = 2².3; ƯCLN(8; 12) = 2² = 4

\(x\) \(\in\) Ư(4) = {-4; - 2; -1; 1; 2; 4}

b, 120⋮ \(x\); 90 \(⋮\) \(x\) 

⇒ \(x\) \(\in\) ƯC(120; 90)

120 =  2³.3.5; 90 = 2.3².5; ƯCLN(120; 90) =  2.3.5 = 30

\(x\) \(\in\)Ư(30) = {-30; -15; -10; -6; - 5; -3; -2; -1; 1; 2; 3; 5;6; 10; 15; 30}

Vì - 5 < \(x\) < 10

Nên \(x\) \(\in\) {-3; -2; -1; 1; 2; 3; 5; 6}

Bổ sung thêm điều kiện của đề: Số cây trồng được của mỗi nhóm là như nhau

Giải

Gọi x (cây) là số cây trồng được của mỗi nhóm (x ∈ ℕ và 200 < x < 250)

Theo đề bài ta có x ∈ BC(8; 9; 12)

Ta có:

8 = 2³

9 = 3²

72 = 2³.3²

⇒ BCNN(8; 9; 72) = 2³.3² = 72

⇒ x ∈ BC(8; 9; 72) = B(72) = {0; 72; 144; 216; 288; ...}

Mà 200 < x < 250 nên x = 216

Vậy số cây trồng được của mỗi nhóm là 216 cây

mình cần gấp

Lời giải:

Vì $ƯCLN(a,b)=16, a>b$ nên đặt $a=16x, b=16y$ với $x,y$ là stn, $x>y$ và $(x,y)=1$

Ta có:

$ab=96$

$\Rightarrow 16x.16y=96$

$\Rightarrow xy=96:16:16=\frac{3}{8}\not\in\mathbb{N}$

Bạn xem lại đề.

Lời giải:

$-2(12-5x)^3=-686$

$(12-5x)^3=-686:(-2)=343=7^3$

$\Rightarrow 12-5x=7$

$\Rightarrow 5x=5$

$\Rightarrow x=1$

Ko biết đâu

Vì hai dấu âm sẽ phải đổi thành hai dâu cộng nên cho dễ hiểu ngta thường lấy dấu công làm sô dương

VD:

9.2.(âm 7).(âm 5)

=2.(âm 5).9.(âm 7)

=âm 10 . âm 63

=630

Lời giải:

$A=(21-23)+(25-27)+....+(2021-2023)$

$=(-2)+(-2)+...+(-2)$

Số lần xuất hiện của $-2$ là: $[(2023-21):2+1]:2=501$

$A=501(-2)=-1002$

$B=(1-2-3+4)+(5-6-7+8)+....+(1997-1998-1999+2000)$

$=0+0+0+...+0=0$

Lời giải:
$=[(-2)+(-4)+6+8]+[(-10)+(-12)+14+16]+...+[(-90)+(-92)+94+96]+98+100$

$=8+8+....+8+198$

Số lần xuất hiện của 8: $[(96-2):2+1]:4=12$

Giá trị của biểu thức là: $8\times 12+198=294$

=

olm chào em, Vấn đề em hỏi olm xin chia sẻ như sau.

Với tài khoản thường thì em có thể học miễn phí mỗi ngày 10 bài luyện tập của olm em nhé.

Trường hợp em muốn sử dụng toàn bộ học liệu của olm thì em vui lòng nâng cấp vip.

Quyền lợi của vip là:

+ Sử dụng toàn bộ học liệu của olm

+ Luyện không giới hạn bài giảng, bài tập của olm

+ Tương tác với giáo viên olm qua zalo 

+ Hỏi bài không giới hạn trên diễn đàn hỏi đáp olm

+ Không bị làm phiền bởi quảng cáo khi học trong suốt thời gian vip em nhé.

Số học sinh khối 6 của một trường khoảng từ 300 đến 400 học sinh. Mỗi lần xếp hàng 12, hàng 15, hàng 18 đều vừa đủ không thừa ai. Hỏi trường đó khối 6 có bao nhiêu học sinh.

Đ/S: 360 học sinh.