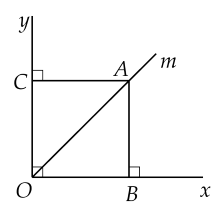
Cho $\widehat{xOy}={{90}^{\circ}}$ và tia phân giác $Om$. Lấy điểm $A$ trên $Om.$ Kẻ $AB, \, AC$ lần lượt vuông góc với $Ox, \, Oy\,.$ Chứng minh $OBAC$ là hình vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`B=y^2-4y+5`
`=y^2-4y+4+1`
`=(y-2)^2+1`
với `y=12` ta có
`(12-2)^2+1=10^2+1=100+1=101`
Với y=12, ta có
12² - 4x12 + 5
= 144 - 48 + 5
= 96 + 5=101

\(f\left(x\right)=x^6+x^3-x^2-1\)
\(f\left(x\right)=x^6-x^3+2x^3-2x^2+x^2-1\)
\(f\left(x\right)=x^3\left(x-1\right)\left(x^2+x+1\right)+2x^2\left(x-1\right)+\left(x-1\right)\left(x+1\right)\)
\(f\left(x\right)=\left(x-1\right)\left(x^5+x^4+x^3+2x^2+x+1\right)\)
Xét đa thức \(g\left(x\right)=x^5+x^4+x^3+2x^2+x+1\) có bậc 5 là số lẻ. Khi đó giả sử tồn tại 2 đa thức \(h\left(x\right)\) và \(j\left(x\right)\) hệ số nguyên sao cho:
\(g\left(x\right)=h\left(x\right).j\left(x\right)\). Khi đó 1 trong 2 đa thức \(h\left(x\right),j\left(x\right)\) phải có bậc lẻ (vì nếu cả 2 đều bậc chẵn thì thành thử bậc của \(g\left(x\right)\) phải chẵn, mâu thuẫn theo trên).
Không mất tổng quát, giả sử đa thức \(h\left(x\right)\) có bậc lẻ. Khi đó nếu nó có nghiệm hữu tỉ thì gọi nghiệm hữu tỉ này là \(x=\dfrac{p}{q}\left(p,q\inℤ;\left(p,q\right)=1\right)\) thì \(p|1,q|1\) nên \(x=\pm1\). Thử lại, ta thấy 2 nghiệm này đều không thỏa mãn.
Do đó, \(g\left(x\right)\) không có nghiệm vô tỉ nên ta không thể phân tích tiếp \(f\left(x\right)\) thành nhân tử được nữa.

Từ giả thiết : \(a+b=-1\) và \(a^2+b^2=5\)
\(\Rightarrow\left(a+b\right)^2=1\) \(\Rightarrow a^2+2ab+b^2=1\)
\(\Rightarrow5+2ab=1\)
\(\Rightarrow2ab=-4\)
\(\Rightarrow ab=-2\)
Từ gt \(\Rightarrow\)\(\left(a+b\right).\left(a^2+b^2\right)=-5\)
\(\Rightarrow a^3+ab^2+a^2b+b^3=-5\)
\(\Rightarrow\left(a^3+b^3\right)+ab.\left(a+b\right)=-5\)
\(\Rightarrow M+\left(-2\right).\left(-1\right)=-5\)
\(\Rightarrow M+2=-5\)
\(\Rightarrow M=-7\)

Ta có : \(A=x^2+y^2=x^2+2xy+y^2-2xy\)
\(A=\left(x+y\right)^2-2xy\)
Với \(x+y=3\) và \(xy=-10\)
\(\Rightarrow A=3^2-2.\left(-10\right)\)
\(A=9+20\)
\(A=29\)
Tương tự : \(B=x^3+y^3=\left(x+y\right)^3-3xy.\left(x+y\right)\)
\(B=\left(3\right)^3-3.\left(-10\right).3\)
\(B=117\)

Lời giải:
Đặt $xy=a; x+y=b$ thì theo đề ta có:
$a+b=-1$ và $ab=-12$
Ta cần tính: $A=(x+y)^3-3xy(x+y)=b^3-3ab=b^3-3(-12)=b^3+36$
Từ $a+b=-1\Rightarrow a=-b-1$. Thay vào $ab=-12$
$\Rightarrow (-b-1)b=-12$
$\Leftrightarrow (b+1)b=12$
$\Leftrightarrow b^2+b-12=0$
$\Leftrightarrow (b-3)(b+4)=0$
$\Leftrightarrow b=3$ hoặc $b=-4$
Nếu $b=3$ thì $A=3^3+36=63$
Nếu $b=-4$ thì $A=(-4)^3+36=-28$

Lời giải:
$x^2+4x+n=(x^2-2x)+(6x-12)+12+n=x(x-2)+6(x-2)+12+n$
$=(x-2)(x+6)+12+n$
Vậy $x^2+4x+n$ chia $x-2$ được thương là $x+6$ và dư $12+n$
\(AC\perp Oy\) (gt); \(Ox\perp Oy\) (gt) => AC//Oy => AC//OB
C/m tương tự có AB//OC
=> OBAC là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{xOy}=90^o\)
=> OBAC là HCN
Ta có
AC=AB (Tính chất đường phân giác)
=> OBAC là hình vuông
Tứ giác ����OBAC có ba góc vuông: góc B= góc C = góc BOC= 90 độ �^=�^=���^=90∘==
∘
Nên ����OBAC là hình chữ nhật.
Mà �A nằm trên tia phân giác ��OM suy ra ��=��AB=AC.
Khi đó ����OBAC là hình vuông.