Cho tam giác $A B C$. Hai điểm $I, J$ được xác định bởi $\overrightarrow{I A}+3 \overrightarrow{I C}=\overrightarrow{0} ; \overrightarrow{J A}+2 \overrightarrow{J B}+3 \overrightarrow{J C}=\overrightarrow{0}$. Chứng minh ba điểm $I, J, B$ thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


???????????????????????????????????????????????????????????????
b) Ta có :
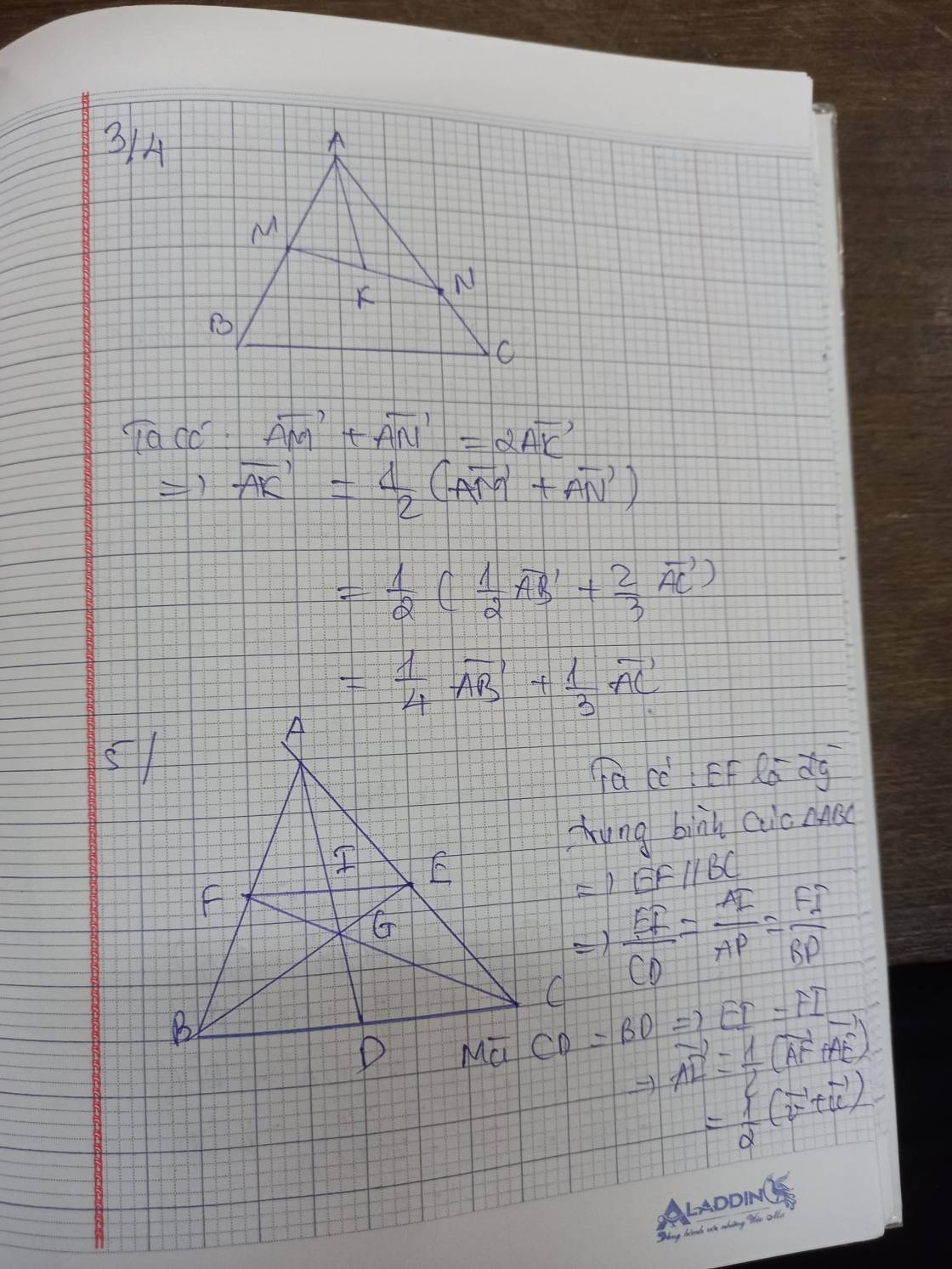
\(IB=2IC\Leftrightarrow IB=2\left(IB+BC\right)\Leftrightarrow-IB=2BC\Leftrightarrow BI=2BC\)
\(JC=-\frac{1}{2}JA\Leftrightarrow JB+BC=-\frac{1}{2}\left(JB+BA\right)\)
\(\Leftrightarrow\frac{3}{2}JB=-\frac{1}{2}BA-BC\Leftrightarrow JB=-\frac{1}{3}BA-\frac{2}{3}BC\)
\(\Rightarrow BJ=\frac{1}{3}BA+\frac{2}{3}BC\)
\(\Rightarrow IJ=BJ-BI=\frac{1}{3}BA+\frac{2}{3}BC-2BC=\frac{1}{3}BA-\frac{4}{3}BC\)
\(KA=-KB\Leftrightarrow KB+BA=-KB\Leftrightarrow2KB=-BA\)
\(\Rightarrow2BK=BA\Leftrightarrow BK=\frac{1}{2}BA\)
\(\Rightarrow JK=BK-BJ=\frac{1}{2}BA-\frac{2}{3}BC=\frac{1}{6}BA-\frac{2}{3}BC\)
\(=\frac{1}{2}\left(\frac{1}{3}BA-\frac{4}{3}BC\right)=\frac{1}{2}IJ\)
Vậy \(I,J,K\)thẳng hàng

TL:
Đáp án:
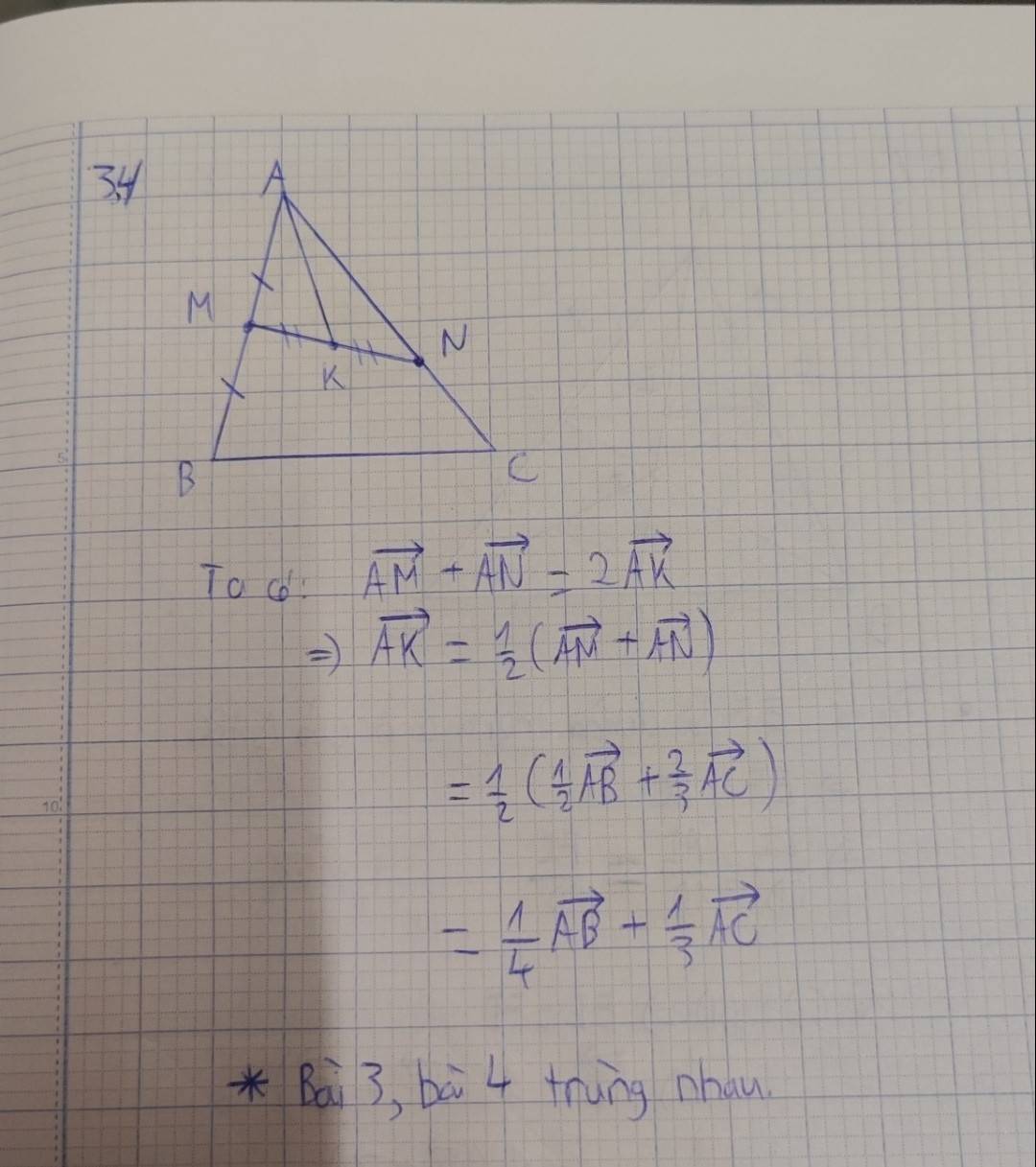
\(\text{KD = KA + AD = - AK + AD }\)
\(=-\frac{1}{2}\left(AM+AN\right)+\frac{1}{2}\left(AB+AC\right)\)
\(=-\frac{1}{2}\left(\frac{1}{2}AB+\frac{2}{3}AC\right)+\frac{1}{2}AB+\frac{1}{2}AC\)
\(=\frac{1}{4}AB+\frac{1}{6}AC\)
HT