Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left(\dfrac{2}{3}\right)^5=\dfrac{2^5}{3^5}=\dfrac{32}{243}\)
\(\left(-\dfrac{2}{3}\right)^5=\dfrac{\left(-2\right)^5}{3^5}=\dfrac{-32}{243}\)
\(\left(-1\dfrac{3}{4}\right)^2=\left(-\dfrac{7}{4}\right)^2=\left(\dfrac{7}{4}\right)^2=\dfrac{49}{16}\)
\(\left(-0,1\right)^4=\left(0,1\right)^4=\left(\dfrac{1}{10}\right)^4=\dfrac{1}{10^4}=\dfrac{1}{10000}\)
b: \(\dfrac{90^3}{15^3}=\left(\dfrac{90}{15}\right)^3=6^3=216\)
\(\dfrac{790^4}{79^4}=\left(\dfrac{790}{79}\right)^4=10^4=10000\)
\(\dfrac{3^2}{15^2}=\left(\dfrac{3}{15}\right)^2=\left(\dfrac{1}{5}\right)^2=\dfrac{1}{25}\)
\(\dfrac{\left(-\dfrac{1}{2}\right)^n}{\left(-\dfrac{1}{2}\right)^{n-1}}=\left(-\dfrac{1}{2}\right)^{n-n+1}=\left(-\dfrac{1}{2}\right)^1=-\dfrac{1}{2}\)

Câu 1:
a: \(-\dfrac{9}{51}\cdot\dfrac{17}{6}=\dfrac{-9}{6}\cdot\dfrac{17}{51}=\dfrac{-3}{2}\cdot\dfrac{1}{3}=-\dfrac{1}{2}\)
b: \(-\dfrac{25}{32}\cdot\left(-0,2\right)=\dfrac{25}{32}\cdot0,2=\dfrac{5}{32}\)
c: \(-15,2\cdot3,5=-53,2\)
d: \(-\dfrac{8}{15}\cdot1\dfrac{1}{4}=-\dfrac{8}{15}\cdot\dfrac{5}{4}=-\dfrac{8}{4}\cdot\dfrac{5}{15}=-\dfrac{2}{3}\)
e: \(1\dfrac{2}{5}\cdot\dfrac{-3}{14}=\dfrac{7}{5}\cdot\dfrac{-3}{14}=-\dfrac{21}{70}=-\dfrac{3}{10}\)
f: \(1\dfrac{1}{17}\cdot1\dfrac{1}{36}=\dfrac{18}{17}\cdot\dfrac{37}{36}=\dfrac{18}{36}\cdot\dfrac{37}{17}=\dfrac{37}{17}\cdot\dfrac{1}{2}=\dfrac{37}{34}\)
Câu 2:
a: \(-\dfrac{5}{2}:\dfrac{5}{8}=-\dfrac{5}{2}\cdot\dfrac{8}{5}=-\dfrac{8}{2}=-4\)
b: \(4\dfrac{1}{5}:\left(-2\dfrac{4}{5}\right)=\dfrac{-21}{5}:\dfrac{14}{5}=-\dfrac{21}{5}\cdot\dfrac{5}{14}=-\dfrac{21}{14}=-\dfrac{3}{2}\)
c: \(7:\left(-3,5\right)=-\dfrac{7}{3,5}=-2\)
d: \(-1\dfrac{4}{5}:\dfrac{-3}{4}=\dfrac{-9}{5}\cdot\dfrac{-4}{3}=\dfrac{-9}{3}\cdot\dfrac{-4}{5}=\dfrac{3\cdot4}{5}=\dfrac{12}{5}\)
e: \(4,2:\dfrac{-15}{12}=4,2:\dfrac{-5}{4}=4,2\cdot\dfrac{-4}{5}=-\dfrac{16.8}{5}=-3,36\)
f: \(6\dfrac{9}{11}:\left(-3\right)=-\dfrac{75}{11}\cdot\dfrac{1}{3}=-\dfrac{25}{11}\)

Bài 6:
\(a)P=\dfrac{2}{1\cdot5}+\dfrac{2}{5\cdot9}+...+\dfrac{2}{33\cdot37}+\dfrac{2}{37\cdot41}\\ =\dfrac{1}{2}\cdot\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{33\cdot37}+\dfrac{4}{37\cdot41}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{33}-\dfrac{1}{37}+\dfrac{1}{37}-\dfrac{1}{41}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{41}\right)\\ =\dfrac{1}{2}\cdot\dfrac{40}{41}\\ =\dfrac{20}{41}\\ b)Q=\dfrac{6}{2\cdot9}+\dfrac{6}{9\cdot16}+...+\dfrac{6}{114\cdot121}\\ =\dfrac{6}{7}\cdot\left(\dfrac{7}{2\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{7}{114\cdot121}\right)\\ =\dfrac{6}{7}\cdot\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{114}-\dfrac{1}{121}\right)\\ =\dfrac{6}{7}\cdot\left(\dfrac{1}{2}-\dfrac{1}{121}\right)\\ =\dfrac{6}{7}\cdot\dfrac{119}{242}\\ =\dfrac{51}{121}\)
Bài 5:
a: Để A>0 thì \(\dfrac{2a-1}{-5}>0\)
=>2a-1<0
=>\(a< \dfrac{1}{2}\)
b: Để A<0 thì \(\dfrac{2a-1}{-5}< 0\)
=>2a-1>0
=>2a>1
=>\(a>\dfrac{1}{2}\)
c: Để A=0 thì \(\dfrac{2a-1}{-5}=0\)
=>2a-1=0
=>2a=1
=>\(a=\dfrac{1}{2}\)
Bài 6:
a: \(P=\dfrac{2}{1\cdot5}+\dfrac{2}{5\cdot9}+...+\dfrac{2}{37\cdot41}\)
\(=\dfrac{2}{4}\cdot\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{37\cdot41}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{37}-\dfrac{1}{41}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{41}\right)=\dfrac{1}{2}\cdot\dfrac{40}{41}=\dfrac{20}{41}\)
b: \(Q=\dfrac{6}{2\cdot9}+\dfrac{6}{9\cdot16}+...+\dfrac{6}{114\cdot121}\)
\(=\dfrac{6}{7}\left(\dfrac{7}{2\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{7}{114\cdot121}\right)\)
\(=\dfrac{6}{7}\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{114}-\dfrac{1}{121}\right)\)
\(=\dfrac{6}{7}\left(\dfrac{1}{2}-\dfrac{1}{121}\right)=\dfrac{6}{7}\cdot\dfrac{119}{242}=\dfrac{51}{121}\)

Bài 5:
\(a)\dfrac{3}{5}\cdot\dfrac{6}{7}+\dfrac{3}{7}:\dfrac{5}{3}-\dfrac{2}{7}:1\dfrac{2}{3}\\ =\dfrac{3}{5}\cdot\dfrac{6}{7}+\dfrac{3}{7}\cdot\dfrac{3}{5}-\dfrac{2}{7}:\dfrac{5}{3}\\ =\dfrac{3}{5}\cdot\dfrac{6}{7}+\dfrac{3}{7}\cdot\dfrac{3}{5}-\dfrac{2}{7}\cdot\dfrac{3}{5}\\ =\dfrac{3}{5}\cdot\left(\dfrac{6}{7}+\dfrac{3}{7}-\dfrac{2}{7}\right)\\ =\dfrac{3}{5}\cdot\dfrac{7}{7}\\=\dfrac{3}{5}\)
\(b)\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)+\dfrac{4}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)\\ =\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{10}{15}\right)+\dfrac{4}{9}:\left(\dfrac{2}{22}-\dfrac{5}{22}\right)\\ =\dfrac{4}{9}:\dfrac{-9}{15}+\dfrac{4}{9}:\dfrac{-3}{22}\\ =\dfrac{4}{9}\cdot\dfrac{-5}{3}+\dfrac{4}{9}\cdot\dfrac{-22}{3}\\ =\dfrac{4}{9}\cdot\left(\dfrac{-5}{3}+\dfrac{-22}{3}\right)\\ =\dfrac{4}{9}\cdot\dfrac{-27}{3}\\ =\dfrac{4}{9}\cdot\left(-9\right)\\ =-4\)
Bài 4:
a: \(-1\dfrac{2}{5}\cdot x=\dfrac{2}{3}-\dfrac{4}{5}\)
=>\(x\cdot\dfrac{-7}{5}=\dfrac{10}{15}-\dfrac{12}{15}=-\dfrac{2}{15}\)
=>\(x=\dfrac{-2}{15}:\dfrac{-7}{5}=\dfrac{2}{15}\cdot\dfrac{5}{7}=\dfrac{2}{21}\)
b: \(\dfrac{2}{3}-4x=\dfrac{1}{2}-\dfrac{2}{5}\)
=>\(\dfrac{2}{3}-4x=\dfrac{5}{10}-\dfrac{4}{10}=\dfrac{1}{10}\)
=>\(4x=\dfrac{2}{3}-\dfrac{1}{10}=\dfrac{20}{30}-\dfrac{3}{30}=\dfrac{17}{30}\)
=>\(x=\dfrac{17}{30}:4=\dfrac{17}{120}\)
Bài 5:
a: \(\dfrac{3}{5}\cdot\dfrac{6}{7}+\dfrac{3}{7}:\dfrac{5}{3}-\dfrac{2}{7}:1\dfrac{2}{3}\)
\(=\dfrac{3}{5}\cdot\dfrac{6}{7}+\dfrac{3}{7}\cdot\dfrac{3}{5}-\dfrac{2}{7}:\dfrac{7}{3}\)
\(=\dfrac{18+9}{35}-\dfrac{2}{7}\cdot\dfrac{3}{7}=\dfrac{27}{35}-\dfrac{6}{49}=\dfrac{159}{245}\)
b: \(\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)+\dfrac{4}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{10}{15}\right)+\dfrac{4}{9}:\left(\dfrac{2}{22}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\dfrac{-9}{15}-\dfrac{4}{9}:\dfrac{-3}{22}\)
\(=\dfrac{4}{9}\cdot\dfrac{-5}{3}+\dfrac{4}{9}\cdot\dfrac{22}{3}=\dfrac{-20+88}{27}=\dfrac{68}{27}\)

a: \(0,5^{1000}=\left(0,5^5\right)^{200}=\left(0,03125\right)^{200}\)
mà \(0,03125< 0,625\)
nên \(0,5^{1000}< 0,625^{200}\)
b: \(\left(-32\right)^{27}=-32^{27}< 0;\left(-27\right)^{32}>0\)
Do đó: \(\left(-32\right)^{27}< \left(-27\right)^{32}\)
c: \(A=2+2^2+...+2^{2022}\)
=>\(2A=2^2+2^3+...+2^{2023}\)
=>\(2A-A=2^2+2^3+...+2^{2023}-2-2^2-...-2^{2022}\)
=>\(A=2^{2023}-2=B-2\)
=>A<B

\(-\left|\dfrac{1}{2}x-2\right|+\dfrac{-2}{3}=\dfrac{-6}{5}\\ \Rightarrow-\left|\dfrac{1}{2}x-2\right|=\dfrac{-6}{5}+\dfrac{2}{3}\\ \Rightarrow-\left|\dfrac{1}{2}x-2\right|=-\dfrac{8}{15}\\ \Rightarrow\left|\dfrac{1}{2}x-2\right|=\dfrac{8}{15}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-2=\dfrac{8}{15}\\\dfrac{1}{2}x-2=-\dfrac{8}{15}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}x=\dfrac{38}{15}\\\dfrac{1}{2}x=\dfrac{22}{15}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{76}{15}\\x=\dfrac{44}{15}\end{matrix}\right.\)
#$\mathtt{Toru}$
\(-\left|\dfrac{1}{2}x-2\right|+\left(-\dfrac{2}{3}\right)=-\dfrac{6}{5}\\ =>-\left|\dfrac{1}{2}x-2\right|=-\dfrac{6}{5}+\dfrac{2}{3}\\ =>-\left|\dfrac{1}{2}x-2\right|=-\dfrac{8}{15}\\ =>\left|\dfrac{1}{2}x-2\right|=\dfrac{8}{15}\)
TH1: \(\dfrac{1}{2}x-2=\dfrac{8}{15}\left(x\ge4\right)\)
\(\Rightarrow\dfrac{1}{2}x=\dfrac{8}{15}+2=\dfrac{38}{15}\\ \Rightarrow x=\dfrac{38}{15}\cdot2=\dfrac{76}{15}\left(tm\right)\)
TH2: \(\dfrac{1}{2}x-2=-\dfrac{8}{15}\left(x< 4\right)\)
\(\Rightarrow\dfrac{1}{2}x=-\dfrac{8}{15}+2=\dfrac{22}{15}\\ \Rightarrow x=\dfrac{22}{15}\cdot2=\dfrac{44}{15}\left(tm\right)\)

a: \(-\dfrac{25}{20}< 0;0< \dfrac{20}{25}\)
Do đó: \(-\dfrac{20}{25}< \dfrac{20}{25}\)
b: \(\dfrac{15}{21}=\dfrac{15:3}{21:3}=\dfrac{5}{7};\dfrac{21}{49}=\dfrac{21:7}{49:7}=\dfrac{3}{7}\)
mà 5>3
nên \(\dfrac{15}{21}>\dfrac{21}{49}\)
c: \(\dfrac{-19}{49}=\dfrac{-19\cdot47}{49\cdot47}=\dfrac{-893}{49\cdot47}\)
\(\dfrac{-23}{47}=\dfrac{-23\cdot49}{47\cdot49}=\dfrac{-1127}{47\cdot49}\)
mà -893>-1127
nên \(-\dfrac{19}{49}>-\dfrac{23}{47}\)

a: ĐKXĐ: \(n\ne4\)
Để A là số nguyên thì \(3n+9⋮n-4\)
=>\(3n-12+21⋮n-4\)
=>\(21⋮n-4\)
=>\(n-4\in\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
=>\(n\in\left\{5;3;7;1;11;-3;25;-17\right\}\)
b: ĐKXĐ: \(n\ne\dfrac{1}{2}\)
Để B là số nguyên thì \(6n+5⋮2n-1\)
=>\(6n-3+8⋮2n-1\)
=>\(8⋮2n-1\)
=>\(2n-1\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
mà 2n-1 lẻ(do n là số nguyên)
nên \(2n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{1;0\right\}\)
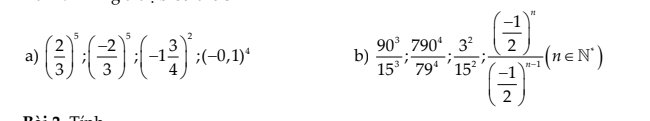




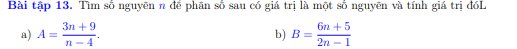
a: \(\left(\dfrac{2}{3}\right)^6\cdot\left(\dfrac{8}{27}\right)^2=\left(\dfrac{2}{3}\right)^6\cdot\left(\dfrac{2}{3}\right)^6=\left(\dfrac{2}{3}\right)^{12}\)
b: \(\left(\dfrac{3}{5}\right)^2\cdot\left(-\dfrac{9}{25}\right)^2=\left(\dfrac{3}{5}\right)^2\cdot\left(\dfrac{9}{25}\right)^2\)
\(=\left(\dfrac{3}{5}\right)^2\cdot\left(\dfrac{3}{5}\right)^4=\left(\dfrac{3}{5}\right)^6\)
c: \(\left(-\dfrac{5}{2}\right)^3:\left(-\dfrac{8}{125}\right)^3\)
\(=\left(-\dfrac{5}{2}:\dfrac{-8}{125}\right)^3=\left(\dfrac{5}{2}\cdot\dfrac{125}{8}\right)^3=\left(\dfrac{625}{16}\right)^3\)
\(=\left(\dfrac{5}{2}\right)^{12}\)