Giải giúp mình bài này với ạ! 6/(x-2) - 12/ [x (x-2)] - 7/x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\frac{\left(x^3\right)^2-\left(y^3\right)^2}{\left[\left(x^2\right)^2-\left(y^2\right)^2\right]-xy\left(x^2-y^2\right)}=\)
\(=\frac{\left(x^3-y^3\right)\left(x^3+y^3\right)}{\left(x^2-y^2\right)\left(x^2+y^2\right)-xy\left(x^2-y^2\right)}=\)
\(=\frac{\left(x+y\right)\left(x^2-xy+y^2\right)\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x^2-y^2\right)\left(x^2+y^2-xy\right)}=\)
\(=\frac{\left(x^2-y^2\right)\left(x^2-xy+y^2\right)\left(x^2+xy+y^2\right)}{\left(x^2-y^2\right)\left(x^2-xy+y^2\right)}=x^2+xy+y^2\)



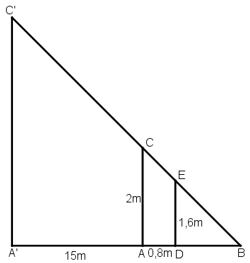
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB 
Vậy cây cao 9,5m.

\(x^2\left(x+1\right)-\left(x+1\right)\left(3x+1\right)+7x-x^2\)
\(=x^3+x^2-3x^2-4x-1+7x-x^2\)
\(=x^3-3x^2+3x-1\)
\(=\left(x-1\right)^3\)

\(A=\frac{2y^2+6y+6}{y^2+4y+5}\)
\(\Leftrightarrow A=\frac{y^2+y^2+4y+2y+5+1}{y^2+4y+5}\)
\(\Leftrightarrow A=\frac{\left(y^2+2y+1\right)+\left(y^2+4y+5\right)}{y^2+4y+5}\)
\(\Leftrightarrow A=1+\frac{\left(y+1\right)^2}{y^2+4y+5}\)
Vì \(1+\frac{\left(y+1\right)^2}{y^2+4y+5}\)> 0
=> \(1+\frac{\left(y+1\right)^2}{y^2+4y+5}\) > 1
Dấu '=' xảy ra khi và chỉ khi y=-1 ( vì (y+1)^2=0 thì 1+0=1=> y=-1)
Vậy Amax=1 khi y=-1

Answer:
\(25x^2-10x+4y-4y^2\)
\(=25x^2-10x+1-4x^2+4y-1\)
\(=\left(25x^2-10x+1\right)-\left(4y^2-2y+1\right)\)
\(=[\left(5x\right)^2-2.5x.1+1]-[\left(2y\right)^2-2.2y.1+1]\)
\(=\left(5x-1\right)^2-\left(2y-1\right)^2\)
\(=\left(5x-1-2y+1\right).\left(5x-1+2y-1\right)\)
\(=\left(5x-2y\right).\left(5x+2y-2\right)\)


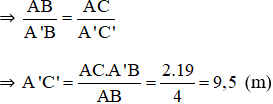
cái này đặt MTC hay j huh bn ?
bài này bn quy đồng mẫu xong tính là ok nhé
mik hướng dẫn bn thôi mik hông vt lại lên đây đâu mik lười lắm có chỗ nào ko lm đc thì gửi mik mik giúp nha
HT~~~