a/

Ta có

EF//AC (gt); GH//AC (gt) => EF//GH (1)

Xét tg ABC có

AE=BE (gt)

EF//AC (gt)

=> BF=CF (trong tg đường thẳng đi qua trung điểm của 1 cạnh ; // với 1 cạnh thì đi qua trung điểm cạnh còn lại)

=> EF là đường trung bình của tg ABC \(\Rightarrow EF=\dfrac{AC}{2}\) (2)

Xét tg BCD chứng minh tương tự => CG=DG

Xét tg ACD chứng minh tương tự => AH=DH

=> GH là đường trung bình của tg ACD \(\Rightarrow GH=\dfrac{AC}{2}\) (3)

Từ (2) và (3) => EF=GH (4)

Từ (1) và (4) => EFGH là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

b/

EFGH là hình chữ nhật \(\Rightarrow\widehat{EFG}=90^o\Rightarrow EF\perp FG\)

Mà FG//BD (gt)

\(\Rightarrow EF\perp BD\) mà EF//AC (gt) \(\Rightarrow AC\perp BD\)

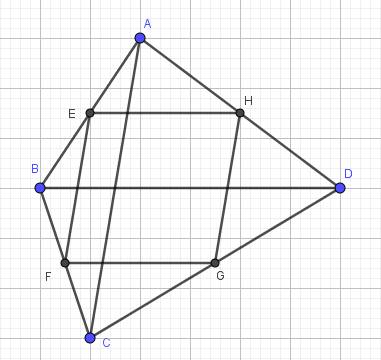
a) \(\Delta ABC\) có:

E là trung điểm của AB (gt)

EF // AC (gt)

\(\Rightarrow\) F là trung điểm của BC

\(\Rightarrow\) EF là đường trung bình của \(\Delta ABC\)

\(\Rightarrow EF=\dfrac{AC}{2}\) (1)

\(\Delta BCD\) có:

F là trung điểm của BC (cmt)

FG // BD (gt)

\(\Rightarrow\) G là trung điểm của CD

\(\Delta ACD\) có:

G là trung điểm của CD (cmt)

GH // AC (gt)

\(\Rightarrow\) H là trung điểm của AD

\(\Rightarrow\) GH là đường trung bình của \(\Delta ACD\)

\(\Rightarrow\) \(GH=\dfrac{AC}{2}\) (2)

Từ (1) và (2) \(\Rightarrow EF=GH\)

Do EF // AC (gt)

GH // AC (gt)

\(\Rightarrow\) EF // GH

Tứ giác EFGH có:

EF // GH (cmt)

EF = GH (cmt)

\(\Rightarrow EFGH\) là hình bình hành

b) Để EFGH là hình chữ nhật thì \(EF\perp FG\)

Lại có:

EF // AC (gt)

FG // BD (gt)

\(\Rightarrow AC\perp BD\)

Vậy \(AC\perp BD\) thì EFGH là hình chữ nhật

a/

Xét tứ giác BMCD có

NB=NC (gt)

ND=NM (gt)

=> BMCD là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

b/

Để BMCD là hình thoi \(\Rightarrow MD\perp BC\) (Hình thoi có 2 đường chéo vuông góc) (1)

Ta có

MA=MC (gt)

NB=NC (gt)

=> MN là đường trung bình của tg ABC => MN//AB => MD//AB (2)

Từ (1) và (2) \(\Rightarrow AB\perp BC\)

Để BMCD là hình thoi => tg ABC là tg vuông tại B

a) Tứ giác BMCD có:

N là trung điểm của BC (gt)

N là trung điểm của DM (gt)

\(\Rightarrow\) BMCD là hình bình hành

b) Để BMCD là hình thoi thì \(BC\perp DM\)

Ta có:

M là trung điểm của AC (gt)

N là trung điểm của BC (gt)

\(\Rightarrow MN\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MN\) // \(AB\)

\(\Rightarrow DM\) // \(AB\)

Mà \(DM\perp BC\)

\(\Rightarrow BC\perp AB\)

Vậy để BMCD là hình thoi thì \(\Delta ABC\) vuông tại B

MN//PQ (cạnh đối hbh) => MI//KQ

Ta có

\(MI=\dfrac{MN}{2};KQ=\dfrac{PQ}{2}\) Mà MN=PQ (cạnh đối hbh) => MI=KQ

=> MIKQ là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

b/

Ta có

MA=MQ (gt) (1)

\(MN=2MQ\left(gt\right)\Rightarrow MQ=\dfrac{MN}{2}\) (2)

Ta có

\(MI=\dfrac{MN}{2}\) (3)

Từ (1) (2) (3) \(\Rightarrow MA=MI=\dfrac{MN}{2}\) => tg AMI cân tại M

Ta có

\(\widehat{AMI}=\widehat{AMP}-\widehat{M}=180^o-120^o=60^o\)

Xét tg AMI có

\(\widehat{MAI}+\widehat{MIA}+\widehat{AMI}=180^o\)

\(\Rightarrow\widehat{MAI}+\widehat{MIA}=180^o-\widehat{AMI}=180^o-60^o=120^o\)

Mà \(\widehat{MAI}=\widehat{MIA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\dfrac{120^o}{2}=60^o\)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\widehat{AMI}=60^o\Rightarrow\Delta AMI\) là tg đều

c/

Xét hbh MNPQ có

MQ//NP => MA//NP

MA=MQ (gt); MQ=NP (cạnh đối hbh)

=> MA=NP

=> APMN là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

Ta có

\(MI=AI=\dfrac{MN}{2}\)  (cạnh tg đều)

\(NI=\dfrac{MN}{2}\)

\(\Rightarrow AI=NI=\dfrac{MN}{2}\) => tg AIN cân tại I

Ta có \(\widehat{AIN}=\widehat{MIN}-\widehat{AIM}=180^o-60^o=120^o\)

Xét tg cân AIN có

\(\widehat{AIN}+\widehat{IAN}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{IAN}+\widehat{INA}=180^o-\widehat{AIN}=180^o-120^o=60^o\)

Mà \(\widehat{IAN}=\widehat{INA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{IAN}=\widehat{INA}=\dfrac{60^o}{2}=30^o\)

Xét tg AMN có

\(\widehat{MAN}+\widehat{AMI}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{MAN}=180^o-\widehat{AMI}-\widehat{INA}=180^o-60^o-30^o=90^o\)

=> APMN là hình chữ nhật (hình bình hành có 1 góc vuông là HCN

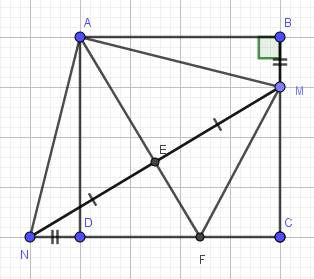
a) Do ABCD là hình vuông (gt)

\(\Rightarrow AB=AD\)

\(\widehat{ABM}=\widehat{ADN}=90^0\)

Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:

\(AB=AD\left(cmt\right)\)

\(BM=DN\left(gt\right)\)

\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)

\(\Rightarrow AM=AN\) (hai cạnh tương ứng)

\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)

Ta có:

\(\widehat{BAM}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{MAN}=90^0\)

\(\Delta AMN\) có:

\(AM=AN\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) cân tại A

Mà \(\widehat{MAN}=90^0\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) vuông cân tại A

b) Do \(\Delta AMN\) cân tại A

E là trung điểm của MN

\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)

\(\Rightarrow AE\perp MN\)

\(\Rightarrow EF\perp MN\)

Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:

\(EM=EN\left(gt\right)\)

\(EF\) là cạnh chung

\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)

\(\Rightarrow FM=FN\) (hai cạnh tương ứng)

Xét \(\Delta FAN\) và \(\Delta FAM\) có:

\(FA\) là cạnh chung

\(FN=FM\left(cmt\right)\)

\(AN=AM\left(cmt\right)\)

\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)

Ta có \(A=-x^2+2xy-4y^2+2x+10y-3\) 

\(A=-x^2+2\left(y+1\right)x-4y^2+10y-3\)

\(A=-x^2+2\left(y+1\right)x-\left(y+1\right)^2-3y^2+12y-2\)

\(A=-\left[x-\left(y+1\right)\right]^2-3\left(y^2-4y+4\right)+10\)

\(A=-\left(x-\left(y+1\right)\right)^2-3\left(y-2\right)^2+10\) \(\le10\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=y+1\\y-2=0\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(3,2\right)\)

Vậy \(max_A=10\)

?

x - y = 2 => x = y + 2 thay vào bt C, ta đc :

C = 2(y+2)^2 - y

= 2(y^2 + 4y + 4) - y

= 2(y^2 + 7/2 .y + 2)

= 2(y+7/4)^2 - 17/8 ≥ -17/8

=> Min = -17/8 tại y = -7/4, x =1/4

giúp mình bài này với

Đề bài là gì vậy bạn?