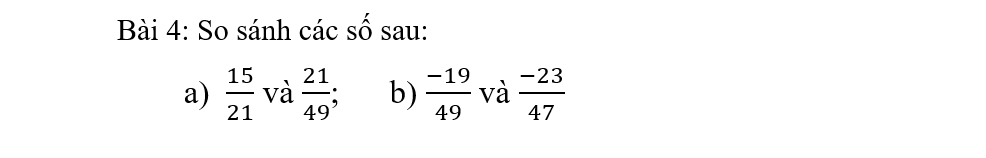
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{998}{555}=\dfrac{555+443}{555}=1+\dfrac{443}{555}\)
\(\dfrac{999}{556}=\dfrac{556+443}{556}=1+\dfrac{443}{556}\)
mà \(\dfrac{443}{555}>\dfrac{443}{556}\)
nên \(\dfrac{998}{555}>\dfrac{999}{556}\)
b: \(\dfrac{315}{380}=1-\dfrac{65}{380};\dfrac{316}{381}=1-\dfrac{65}{381}\)
Ta có: 380<381
=>\(\dfrac{65}{380}>\dfrac{65}{381}\)
=>\(-\dfrac{65}{380}< -\dfrac{65}{381}\)
=>\(-\dfrac{65}{380}+1< -\dfrac{65}{381}+1\)
=>\(\dfrac{315}{380}< \dfrac{316}{381}\)
=>\(-\dfrac{315}{380}>-\dfrac{316}{381}\)

a: \(\dfrac{7}{8}=\dfrac{7\cdot3}{8\cdot3}=\dfrac{21}{24};\dfrac{11}{12}=\dfrac{11\cdot2}{12\cdot2}=\dfrac{22}{24}\)
mà 21<22
nên \(\dfrac{7}{8}< \dfrac{11}{12}\)
b: \(\dfrac{-5}{8}=\dfrac{-5\cdot5}{8\cdot5}=\dfrac{-25}{40};\dfrac{7}{-10}=\dfrac{-7}{10}=\dfrac{-7\cdot4}{10\cdot4}=\dfrac{-28}{40}\)
mà -25>-40
nên \(-\dfrac{5}{8}>\dfrac{7}{-10}\)

a: \(\dfrac{24}{35}=\dfrac{24\cdot6}{35\cdot6}=\dfrac{144}{210};\dfrac{19}{30}=\dfrac{19\cdot7}{30\cdot7}=\dfrac{133}{210}\)
b: \(\dfrac{-9}{21}=\dfrac{-9:3}{21:3}=\dfrac{-3}{7};\dfrac{27}{-63}=\dfrac{27:\left(-9\right)}{-63:\left(-9\right)}=\dfrac{-3}{7}\)
Do đó: \(\dfrac{-9}{21}=\dfrac{27}{-63}\)

a: \(\dfrac{9}{70}=\dfrac{9\cdot3}{70\cdot3}=\dfrac{27}{210};\dfrac{5}{42}=\dfrac{5\cdot5}{42\cdot5}=\dfrac{25}{210}\)
mà 27>25
nên \(\dfrac{9}{70}>\dfrac{5}{42}\)
b: \(\dfrac{-4}{27}=\dfrac{-4\cdot7}{27\cdot7}=\dfrac{-28}{189};\dfrac{15}{-63}=\dfrac{-15}{63}=\dfrac{-15\cdot3}{63\cdot3}=\dfrac{-45}{189}\)
mà -28>-45
nên \(-\dfrac{4}{27}>-\dfrac{15}{63}\)

\(a)\left(\dfrac{2}{3}\right)^5=\dfrac{2^5}{3^5}=\dfrac{32}{243}\\ \left(\dfrac{-2}{3}\right)^5=\dfrac{\left(-2\right)^5}{3^5}=\dfrac{-32}{243}\\ \left(-1\dfrac{3}{4}\right)^2=\left(-\dfrac{7}{4}\right)^2=\dfrac{\left(-7\right)^2}{4^2}=\dfrac{49}{16}\\ \left(-0,1\right)^4=\left(-\dfrac{1}{10}\right)^4=\dfrac{\left(-1\right)^4}{10^4}=\dfrac{1}{10000}\)
\(b)\dfrac{90^3}{15^3}=\left(\dfrac{90}{15}\right)^3=6^3=216\\ \dfrac{790^4}{79^4}=\left(\dfrac{790}{79}\right)^4=10^4=10000\\ \dfrac{3^2}{15^2}=\left(\dfrac{3}{15}\right)^2=\left(\dfrac{1}{5}\right)^2=\dfrac{1^2}{5^2}=\dfrac{1}{25}\\ \dfrac{\left(-\dfrac{1}{2}\right)^n}{\left(-\dfrac{1}{2}\right)^{n-1}}=\left(-\dfrac{1}{2}\right)^{n-\left(n-1\right)}=\left(-\dfrac{1}{2}\right)^{n-n+1}=\left(-\dfrac{1}{2}\right)\)

a) Ta có:
\(\dfrac{13}{15}=\dfrac{15-2}{15}=1-\dfrac{2}{15}\)
\(\dfrac{9}{11}=\dfrac{11-2}{11}=1-\dfrac{2}{11}\)
Vì: \(\dfrac{2}{15}< \dfrac{2}{11}=>1-\dfrac{2}{15}>1-\dfrac{2}{11}=>\dfrac{13}{15}>\dfrac{9}{11}\)
b) Ta có:
\(\dfrac{-9}{17}< 0\)
\(\dfrac{-20}{-21}=\dfrac{20}{21}>0\)
\(=>-\dfrac{9}{17}< 0< \dfrac{20}{21}\)

a) Ta có:
\(\dfrac{11}{6}>1=>-\dfrac{11}{6}< -1\)
\(\dfrac{8}{9}< 1=>-\dfrac{8}{9}>-1\)
\(=>-\dfrac{11}{6}< -1< -\dfrac{8}{9}\)
b) Ta có:
\(\dfrac{-25}{20}< 0\)
\(\dfrac{20}{25}>0\)
\(=>-\dfrac{25}{20}< 0< \dfrac{20}{25}\)

Bài 15:
a: Ta có: \(\widehat{A_1}=\widehat{M_1}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//MN
b: ta có: \(\widehat{NMC}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên MN//CD
Bài 14:
a: Ta có: \(\widehat{H_1}=\widehat{xAH}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Hm//Ax
b: Ta có: \(\widehat{A_1}=\widehat{K_1}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Ax//Kn

\(a)\left(\dfrac{6}{7}+1\dfrac{1}{2}\right)^2\\ =\left(\dfrac{6}{7}+\dfrac{3}{2}\right)^2\\ =\left(\dfrac{12}{14}+\dfrac{21}{14}\right)^2\\ =\left(\dfrac{33}{14}\right)^2\\ =\dfrac{1089}{196}\\ b)\left(2\dfrac{1}{5}-1\dfrac{2}{3}\right)^3\\ =\left(\dfrac{11}{5}-\dfrac{5}{3}\right)^3\\ =\left(\dfrac{33}{15}-\dfrac{25}{15}\right)^3\\ =\left(\dfrac{8}{15}\right)^3\\ =\dfrac{512}{3375}\\ c)3^2+4\cdot\left(\dfrac{7}{9}\right)^0+\left[\left(-5\right)^2:\dfrac{1}{5}\right]:25\\ =9+4\cdot1+\left(5^2\cdot5\right):25\\ =13+5^3:5^2\\ =13+5\\ =18\)

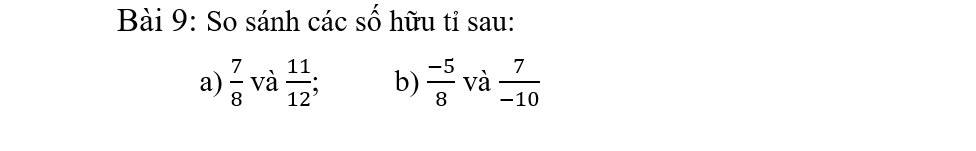




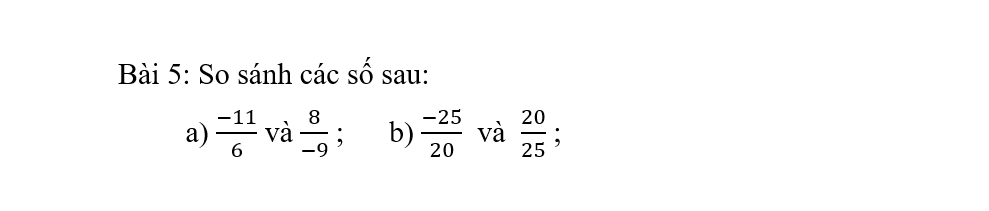

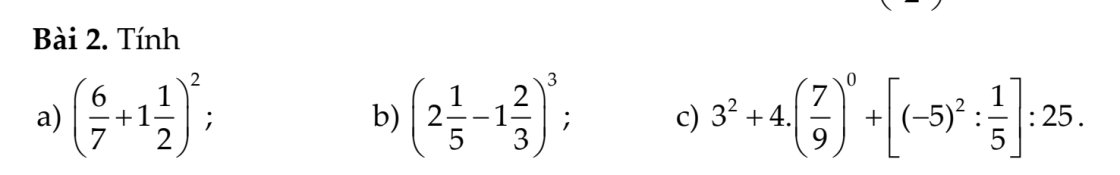
a: \(\dfrac{15}{21}=\dfrac{15:3}{21:3}=\dfrac{5}{7};\dfrac{21}{49}=\dfrac{21:7}{49:7}=\dfrac{3}{7}\)
mà 5>3
nên \(\dfrac{15}{21}>\dfrac{21}{49}\)
b: \(\dfrac{-19}{49}=\dfrac{-19\cdot47}{49\cdot47}=\dfrac{-893}{2303}\)
\(\dfrac{-23}{47}=\dfrac{-23\cdot49}{49\cdot47}=\dfrac{-1127}{2303}\)
mà -893>-1127
nên \(-\dfrac{19}{49}>-\dfrac{23}{47}\)