a) \(4x^2-1=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x\right)^2-1^2=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)\left(3x-5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1-3x+5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(4-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\4=x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=4\end{matrix}\right.\)

Vậy: ...

b) \(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\)

\(\Leftrightarrow\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}-10=0\)

\(\Leftrightarrow\left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0\)

\(\Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\)

\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)

\(\Leftrightarrow x-100=0\)

\(\Leftrightarrow x=100\)

Vậy: ... 

a) Bảng giá trị

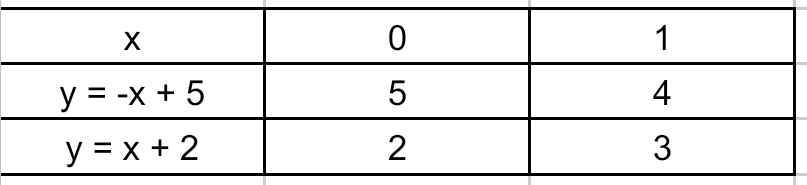  Đồ thị:

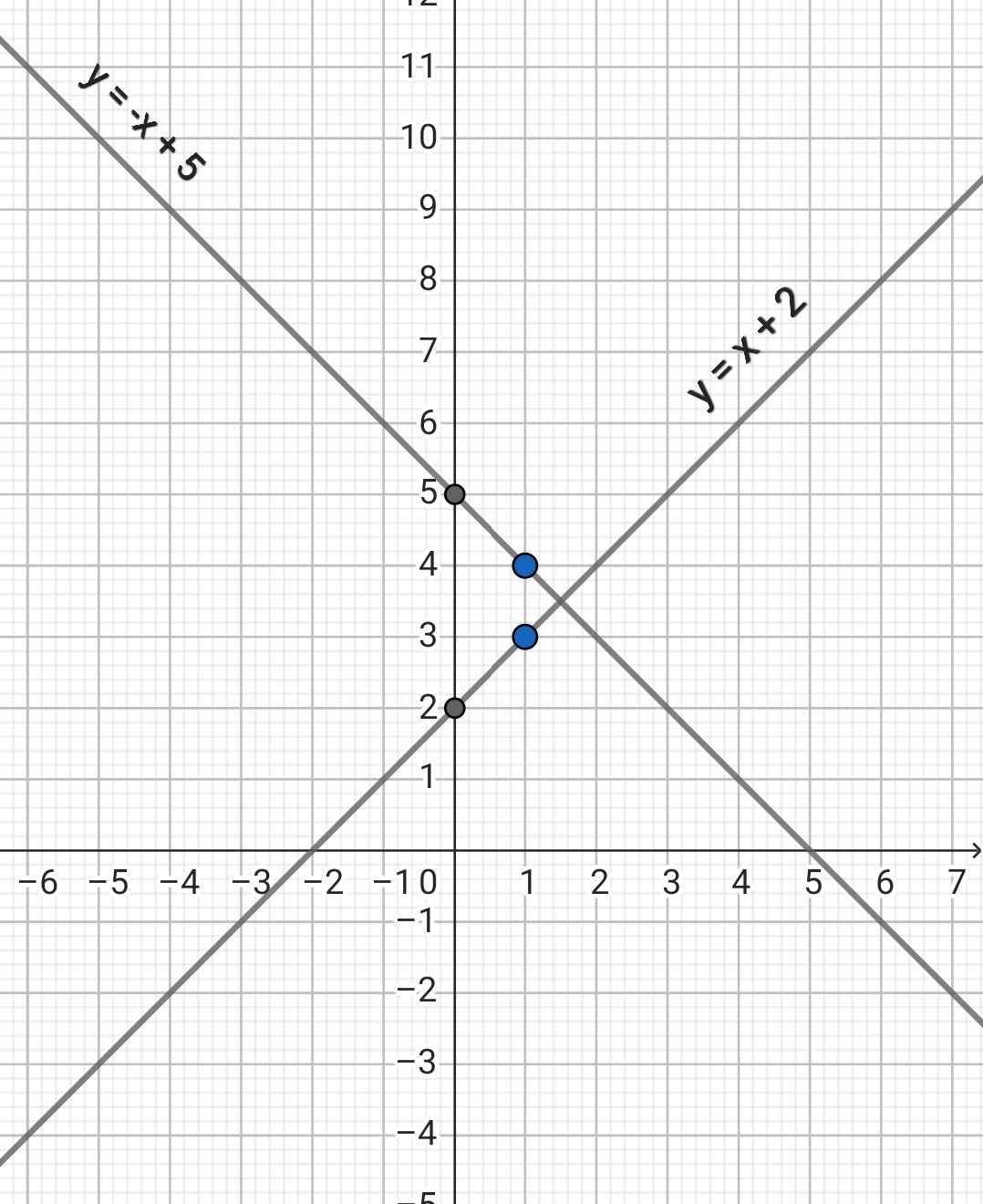
b) Phương trình hoành độ giao điểm của (d₁) và (d₂):

-x + 5 = x + 2

-x - x = 2 - 5

-2x = -3

x = 3/2

Thay x = 3/2 vào (d₂), ta có:

y = 3/2 + 2 = 7/2

Vậy tọa độ giao điểm M(3/2; 7/2)

c) Gọi (d₃): y = ax + b (a ≠ 0) là đồ thị của hàm số cần tìm

Do (d₃) // (d₁) nên a = -1

⇒ (d₃): y = -x + b

Do (d₃) đi qua K(-4; 2) nên thay tọa độ của K(-4; 2) vào (d₃), ta có:

-(-4) + b = 2

b = 2 - 4

b = -2

Vậy hàm số cần tìm là:

y = -x - 2

a) Đồ thị hs:`y=-2x+5` cắt `Ox(5/2;0)` và cắt `Oy(0;5)` 

Đồ thị hs: `y=x+2` cắt `Ox(-2;0)` và cắt `Oy(0;2)` 

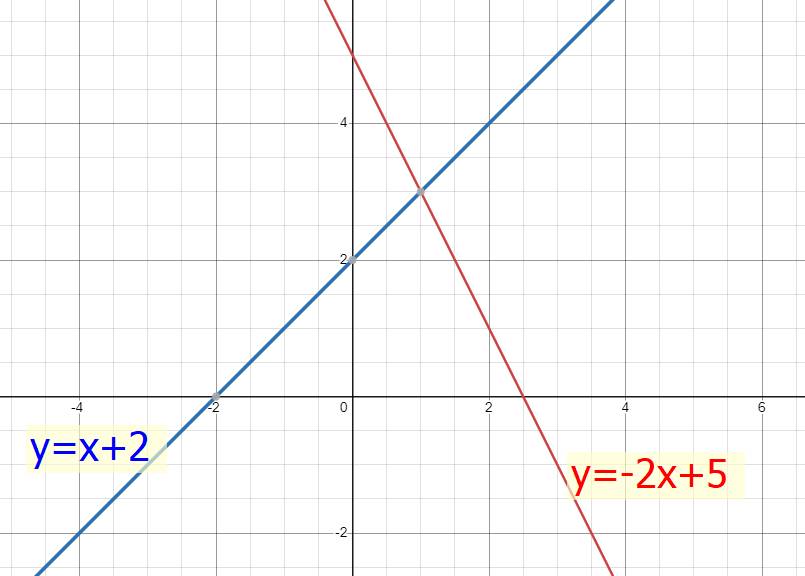
b) Ta có pt hoành độ giao điểm của (d₁) và (d₂): 

\(-2x+5=x+2\)

\(\Leftrightarrow x+2x=5-2\)

\(\Leftrightarrow3x=3\)

\(\Leftrightarrow x=1\)

Thay `x=1` vào `(d_2)` ta có: \(y=1+2=3\)

`=>M(1;3)` 

c) Hàm số `y=ax+b` có đồ thị song song với `(d_1):y=-2x+5` 

`=>a=-2` 

`=>y=-2x+b` 

Mà hàm số này đi qua điểm `K(-4;2)` ta thay `x=-4` và `y=2` vào ta có:

`2=-2*(-4)+b`

`<=>2=8+b`

`<=>b=2-8=-6` 

Vậy hàm số đó là: `y=-2x-6` 

mình đang cần gấp

a: Xét ΔAFB và ΔCFI có

\(\widehat{FAB}=\widehat{FCI}\)(hai góc so le trong, AB//CI)

\(\widehat{AFB}=\widehat{CFI}\)(hai góc đối đỉnh)

Do đó: ΔAFB~ΔCFI

b: Xét ΔEAB và ΔEKD có

\(\widehat{EAB}=\widehat{EKD}\)(hai góc so le trong, AB//KD)

\(\widehat{AEB}=\widehat{KED}\)(hai góc đối đỉnh)

Do đó: ΔEAB~ΔEKD

=>\(\dfrac{AB}{KD}=\dfrac{AE}{KE}\)

=>\(AB\cdot KE=AE\cdot KD\)

a) ta có: M là trung điểm của AB, N là trung điểm BC

\(\Rightarrow MN\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MN\) // \(AC\) hay \(MN\) // \(AD\)

ta có: N là trung điểm BC; D là trung điểm AC

⇒ ND là đường trung bình của \(\Delta ABC\)

⇒ ND // AB hay ND // MA

xét tứ giác NMAD, có:

MN // AD (chứng minh trên)

MA // ND (chứng minh trên)

⇒ tứ giác NMAD là hình bình hành

⇒ MD = AN

b) Xét tứ giác BMDN, có:

\(ND=BM\) (Vì ND là đường trung bình của ΔABC)

Lại có: ND // AB ⇒ ND // BM

⇒ tứ giác BMDN là hình bình hành

Lại có: O là trung điểm của đường chéo MN

⇒ O cũng là trung điểm đường chéo BD

⇒ 3 điểm B; O; D thẳng hàng

a: Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{9}=\dfrac{DC}{12}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

mà DB+DC=BC=15cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{15}{7}\)

=>\(DB=3\cdot\dfrac{15}{7}=\dfrac{45}{7}\left(cm\right);DC=4\cdot\dfrac{15}{7}=\dfrac{60}{7}\left(cm\right)\)

b: Vì \(\dfrac{BD}{CD}=\dfrac{45}{7}:\dfrac{60}{7}=\dfrac{3}{4}\)

nên \(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{3}{4}\)

a: Sửa đề: MH//CD

Xét ΔADC có

M,H lần lượt là trung điểm của AD,AC

=>MH là đường trung bình của ΔADC

=>MH//DC và \(MH=\dfrac{DC}{2}\)

Xét ΔCABcó 

N,H lần lượt là trung điểm của CB,CA

=>NH là đường trung bình của ΔCAB

=>NH//AB và \(NH=\dfrac{AB}{2}\)

b: MH+HN<=MN

=>\(\dfrac{1}{2}\left(AB+CD\right)< =MN\)

=>\(MN>=\dfrac{1}{2}\left(AB+CD\right)\)

a: Xét ΔABC có EI//BC

nên \(\dfrac{AE}{AB}=\dfrac{AI}{AC}\left(1\right)\)

Xét ΔADC có FI//DC

nên \(\dfrac{AI}{AC}=\dfrac{AF}{AD}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{AE}{AB}=\dfrac{AF}{AD}\)

Xét ΔABD có \(\dfrac{AE}{AB}=\dfrac{AF}{AD}\)

nên EF//BD

b: Xét ΔCBA có GI//AB

nên \(\dfrac{CG}{BG}=\dfrac{CI}{IA}\left(3\right)\)

Xét ΔCAD có IH//AD

nên \(\dfrac{CI}{IA}=\dfrac{CH}{HD}\left(4\right)\)

Từ (3),(4) suy ra \(\dfrac{CG}{BG}=\dfrac{CH}{HD}\)

=>\(CG\cdot HD=BG\cdot CH\)

a: Ta có: AK=KO=OH

=>\(AK=KO=OH=\dfrac{1}{3}AH\)

=>\(AO=\dfrac{2}{3}AH;AK=\dfrac{1}{3}AH\)

Xét ΔAHB có EK//BH

nên \(\dfrac{AE}{AB}=\dfrac{AK}{AH}\)

=>\(\dfrac{AE}{AB}=\dfrac{1}{3}\)

Xét ΔABH có MO//BH

nên \(\dfrac{AM}{AB}=\dfrac{AO}{AH}\)

=>\(\dfrac{AM}{AB}=\dfrac{2}{3}\)

Xét ΔABC có EF//BC

nên \(\dfrac{EF}{BC}=\dfrac{AE}{AB}\)

=>\(\dfrac{EF}{BC}=\dfrac{1}{3}\)

=>\(EF=\dfrac{BC}{3}=\dfrac{30}{3}=10\left(cm\right)\)

Xét ΔABC có MP//BC

nên \(\dfrac{MP}{BC}=\dfrac{AM}{AB}\)

=>\(\dfrac{MP}{30}=\dfrac{2}{3}\)

=>\(MP=20\left(cm\right)\)

b: Xét ΔAMP và ΔABC có 

\(\widehat{AMP}=\widehat{ABC}\)(hai góc đồng vị, MP//BC)

\(\widehat{MAP}\) chung

Do đó: ΔAMP~ΔABC

=>\(\dfrac{S_{AMP}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2\)

=>\(\dfrac{S_{AMP}}{10.8}=\dfrac{4}{9}\)

=>\(S_{AMP}=4,8\left(dm^2\right)\)

Xét ΔAEF và ΔABC có

\(\widehat{AEF}=\widehat{ABC}\)(hai góc đồng vị, EF//BC)

\(\widehat{FAE}\) chung

Do đó: ΔAEF~ΔABC

=>\(\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=\dfrac{1}{9}\)

=>\(S_{AEF}=\dfrac{10.8}{9}=1,2\left(dm^2\right)\)

Ta có: \(S_{AEF}+S_{MEFP}=S_{AMP}\)

=>\(S_{MEFP}+1,2=4,8\)

=>\(S_{MEFP}=3,6\left(dm^2\right)\)