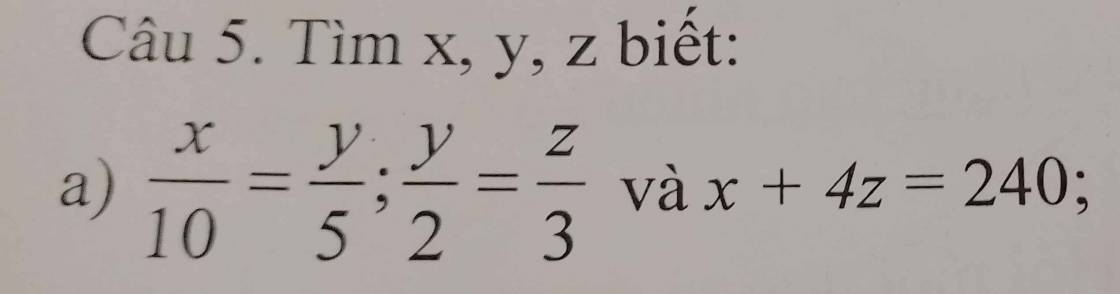Ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}\)  \(\left(1\right)\)
\(\dfrac{y}{2}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{y}{10}=\dfrac{z}{15}\)  \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
Lại có:
\(\dfrac{z}{15}=\dfrac{4z}{60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{4z}{60}=\dfrac{x+4z}{20+60}=\dfrac{240}{80}=3\)
\(\Rightarrow x=3\cdot20=60\)
     \(y=3\cdot10=30\)
     \(z=3\cdot15=45\)

B A D C

Ta có: ∠BAC + ∠DAC = 180° ( kề bù )

mà ∠BAC = 90° (gt)

⇒ ∠DAC = 180° - 90° = 90°

⇒ ∠BAC = ∠DAC

Xét ∆ABC và ∆ADC có: AB = AC (gt)  ; ∠BAC = ∠DAC (cmt) ; AC chung

⇒ ∆ABC = ∆ADC ( c_g_c)

⇒ BC = DC ( 2 cạnh tương ứng )

⇒ ∆CBD cân tại C ( theo dhnb)

Chú thích: 

gt: giả thiết

theo dhnb: dấu hiệu nhận biết

AB= 5cm

BC= 2cm

AC=4cm

MN=5cm

NP=2cm

MP=4cm

A = x² - 3x + x⁴ - 2x + x² + 2

A = x⁴ + ( x² + x²) - (3x + 2x) + 2

A = x⁴ + 2x² - 5x +2

Bậc của đa thức là bậc 4

A(1) = 1⁴ + 2.1² -5.1 + 2

A(1) = 0

a, A = ax² + bx + 1 ( a #0)

b, A = 2x² + 2x + c 

Câu này làm thế nào vậy mn

giúp mình với

xét ΔECB và ΔDBC, ta có : 

EC = BD (gt)

\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)

BC là cạnh chung

=> ΔECB = ΔDBC (c.g.c)

=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)

vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)

H(-1) = 2\(x^2\)- 10 

H(-1) = 2.(-1)² - 10

H(-1) = 2 - 10

H(-1) = -8

H(\(\dfrac{1}{2}\)) = 2\(x^2\) - 10

H(\(\dfrac{1}{2}\)) = 2.(\(\dfrac{1}{2}\))² - 10

H(\(\dfrac{1}{2}\)) = \(\dfrac{1}{2}\) - 10

H(\(\dfrac{1}{2}\)) = \(-\dfrac{19}{2}\)

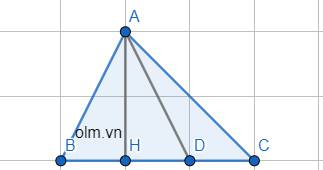
Vì AH \(\perp\) BC  \(\equiv\) H  nên:

BH là hình chiếu của AB trên BC

HC là hình chiếu của AC trên BC

AB < AC => BH < HC ( Mối quan hệ đường xiên và hình chiếu )

\(\widehat{BAH}\) Đối diện cạnh BH

\(\widehat{HAC}\) Đối diện cạnh HC

mà BH < HC ( chứng minh trên)

=> \(\widehat{BAH}\) < \(\widehat{HAC}\) ( mối quan hệ giữa cạnh và góc trong tam giác)

Ta có : HD = HB (gt) (1)

            AH \(\perp\) BD \(\equiv\) H (2)

Từ (1) và (2) ta có : \(\Delta\) ABD cân tại A vì AH vừa là đường cao vừa là đường trung tuyến của \(\Delta\) ABD