So sánh và giải thích : 336 và 512
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Số HS đạt điểm giỏi:
\(42\times\dfrac{1}{7}=6\) (HS)
Số HS đạt điểm khá:
\(42\times\dfrac{2}{7}=12\) (HS)
Số HS đạt điểm trung bình:
\(42\times\dfrac{1}{2}=21\) (HS)
Số HS đạt điểm yếu:
\(42-6-12-21=3\) (HS)
b) Tỉ số giữa HS đạt điểm giỏi và HS đạt điểm TB là:
\(6:21=\dfrac{2}{7}\)
c) Tỉ số phần trăm giữa HS đạt điểm TB so với số HS cả lớp:
\(21:42\times100\%=50\%\)

a) Quy luật:
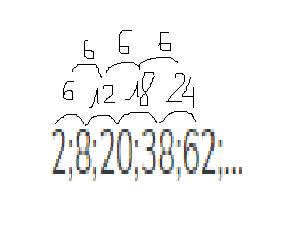
Khoảng cách giữa các khoảng cách của từng số hạng liên tiếp trong dãy số của đề bài là: 6.
b) Ta có dãy số từ khoảng cách của từng số hạng liên tiếp trong đề bài:
6; 12; 18; 24; ...
Khoảng cách giữa 2 số hạng liên tiếp: 6.
Số hạng thứ 49 của dãy mới sẽ được cộng với số hạng thứ 49 của dãy ban đầu (số thứ tự bị giảm do số lượng khoảng cách) = số hạng thứ 50 của dãy ban đầu.
Số hạng thứ 49 của dãy mới là:
6 + 6 x (49 - 1) = 294
Số số hạng của dãy là: 49
Số thứ 5 của dãy là:
2 + (294 + 6) x 49 : 2 = 7352

Mẹ bạn Minh lãi được số tiền là:
\(2062400-2000000=62400\) (đồng)
Số tiền lãi hàng tháng của mẹ bạn Minh là:
\(62400:6=10400\) (đồng)
Lãi suất hàng tháng của thể thức tiết kiệm này là:
\(\frac{10400}{2000000}\cdot 100\%=0,52\%\)

\(\frac{x-1}{1999}+\frac{x-2}{1998}=\frac{x-3}{1997}+\frac{x-4}{1996}\\\Leftrightarrow \left(\frac{x-1}{1999}-1\right) +\left(\frac{x-2}{1998}-1\right)=\left(\frac{x-3}{1997}-1\right)+\left(\frac{x-4}{1996}-1\right)\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}=\frac{x-2000}{1997}+\frac{x-2000}{1996}\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}-\frac{x-2000}{1997}-\frac{x-2000}{1996}=0\\ \Leftrightarrow (x-2000)\left(\frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\right)=0\\\Leftrightarrow x-2000=0\left(\text{vì } \frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\ne0\right)\\\Leftrightarrow x=2000\)
Vậy phương trình đã cho có 1 nghiệm duy nhất là \(x=2000\).

\(x-50\%\times x+60\%\times x=35+0,4\times x\\x-50\%\times x+60\% \times x=35+40\% \times x\\x\times 100\%-50\% \times x+60\% \times x-40\%\times x=35\\x\times(100\%-50\%+60\%-40\%)=35\\x\times(50\%+20\%)=35\\x\times70\%=35\\x=35:70\%\\x=50\)

Olm chào em, Số chẵn bên tay phải và số lẻ ở bên tay trái em nhé.

ĐỐI VỚI BÀI TOÁN LẬP PHƯƠNG TRÌNH VỀ QUÃNG ĐƯỜNG VẬN TỐC THỜI GIAN THÌ NÊN LẬP BẢNG ĐỂ GIẢI DỄ DÀNG HƠN
| vận tốc | quãng đường | thời gian | |
| A - B | x + 10 | 4(x + 10) | 4 |
| B - A | x - 10 | 5(x - 10) | 5 |
vì vận tốc của dòng nước là 10km/h nên:
vận tốc cano đi từ A đến B là: x + 10 (km/h)
vận tốc cano đi từ B đến A là: x - 10 (km/h)
quãng đường cano đi từ A đến B là: 4(x + 10) (km)
quãng đường cano đu từ B đến A là: 5(x - 10) (km)
theo đề ta có phương trình:
4(x + 10) = 5(x - 10)
4x + 40 = 5x - 50
4x - 5x = -40 - 50
-x = -90
x = 90
quãng đường AB dài là: 4(90+10) = 400 (km)
VẬY QUÃNG ĐƯỜNG AB DÀI 400KM
Cùng quãng sông nên vận tốc và thời gian tỉ lệ nghịch
Tỉ số thời gian đi xuôi so với đi ngược là : \(\dfrac{4}{5}\)
=> Tỉ số vận đi xuôi so với đi ngược là : \(\dfrac{5}{4}\)
Ta có sơ đồ:
Vận tốc đi xuôi :|------|------|------|------|------|
Vận tốc đi ngược :|------|------|------|------|
Hiệu vận tốc đi xuôi với đi ngược là:
10 x 2 = 20 (km/giờ)
=> Vận tốc đi xuôi dòng của ca nô là:
20 : (5 - 4) x 5 = 100 (km/giờ)
=> Khoảng cách từ A đến B là:
100 x 4 = 400 (km)
Đ/s: 400 km

A = \(x^2\) + 5\(x\) - 6
A = \(x^2\) - \(x\) + 6\(x\) - 6
A = (\(x^2\) - \(x\)) + (6\(x\) - 6)
A = \(x\).(\(x-1\)) + 6.(\(x-1\))
A = (\(x\) - 1).(\(x\) + 6)

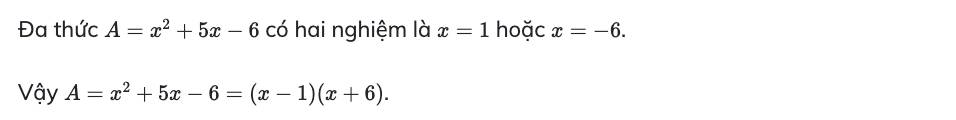
\(3^{36}=3^{3.12}=\left(3^3\right)^{12}=27^{12}>5^{12}\)
Vậy: \(3^{36}>5^{12}\)