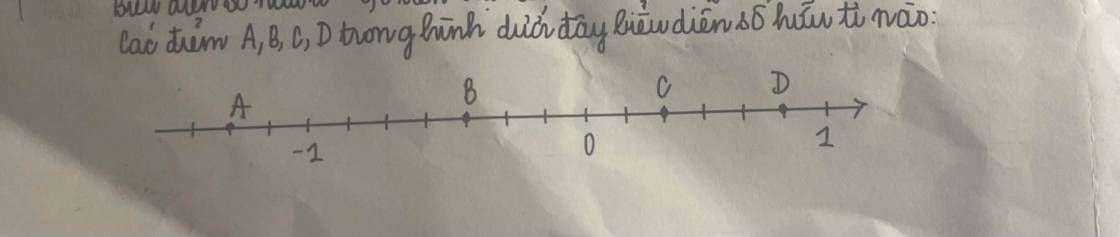A ~ -9/7; B ~ -3/7; C ~ 2/6; D ~ 5/6

2485 á

tick đi

Olm chào em cái này chỉ có thể tìm chữ số tận cùng thôi em. 

Nếu chia 15 dư 6 thì chắc chắn sẽ chia hết cho 3

Nếu chia 9 dư 1 thì chắc chắn sẽ không bao giờ chia hết cho 3

Do đó, hai điều này đối nghịch nhau

Từ đó suy ra, không có số tự nhiên nào chia 15 dư 6 và chia 9 dư 1

Giả sử tồn tại một số a chia cho 15 dư 6 và chia 9 dư 1 khi đó ta có:

 \(\left\{{}\begin{matrix}a=15k+6\left(k\in N\right)\\15k+6-1⋮9\end{matrix}\right.\) ⇒ 15k + 6 - 1 ⋮ 3  ⇒ 15k + 5 ⋮ 3 ⇒ 3.(5k + 1) + 2 ⋮ 3

⇒ 2 ⋮ 3 (vô lí) Điều giả sử là sai. 

Vậy không có số tự nhiên nào mà chia cho 15 dư 6 và chia 9 dư 1

Gọi số cần tìm là a

Số mới là a+60%a=1,6a

Phần trăm cần giảm để về lại số cũ là:

\(\dfrac{1,6a-a}{1,6a}=\dfrac{0.6}{1,6}=\dfrac{6}{16}=37,5\%\)

60% hỏi zô tri qá

a: Vì MB và MC là hai tia đối nhau

nên M nằm giữa B và C

=>BC=BM+CM=4+2=6(cm)

b: Vì BM và BO là hai tia đối nhau

nên B nằm giữa M và O

mà BM=BO(=4cm)

nên B là trung điểm của OM

=>\(OM=2\cdot MB=8\left(cm\right)\)

Vì MC và MO là hai tia đối nhau

nên M nằm giữa C và O

=>OC=CM+MO=2+8=10(cm)

coi S ban đầu,chiều dài và chiều rộng là 100%

Chiều dài sau khi tăng 10 % là : 

100%+10%=110%

Chiều rộng sau khi giảm là :

100%-10%=90%

Sau khi thay đổi thì S là :

110%x90%=99%

giảm số phần trăm là :

100%-99%=1%

Tỉ số giữa chiều dài lúc sau và chiều dài lúc đầu là:

100%+10%=110%=1,1

Tỉ số giữa chiều rộng lúc sau và chiều rộng lúc đầu là:

100%-10%=90%=0,9

Tỉ số giữa diện tích lúc sau và diện tích lúc đầu là:

1,1x0,9=0,99=1-0,01=1-1%

=>Diện tích giảm 1%

1456=1000+400+50+6

9413=9000+400+10+3

6358=6000+300+50+8

3992=3000+900+90+2

a, 1456 = 1000 + 400 + 50 + 6

b, 9413 = 9000 + 400 + 10 + 3

c, 6358 = 6000 + 300 + 50 + 8

d, 3992 = 3000 + 900 + 90 + 2

a: Xét ΔABC có BM là phân giác

nên \(\dfrac{AM}{MC}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)

=>\(\dfrac{AM}{3}=\dfrac{MC}{5}\)

mà AM+MC=AC=6cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AM}{3}=\dfrac{MC}{5}=\dfrac{AM+MC}{3+5}=\dfrac{6}{8}=\dfrac{3}{4}\)

=>\(AM=3\cdot\dfrac{3}{4}=\dfrac{9}{4}\left(cm\right)\)

b: Xét ΔEBC có GQ//BC

nên \(\dfrac{EG}{EB}=\dfrac{EQ}{EC}\)

Xét ΔMBC có QI//BC

nên \(\dfrac{CI}{CM}=\dfrac{BQ}{BM}\)

Ta có: \(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)

\(\widehat{ACE}=\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)

mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)

nên \(\widehat{ABM}=\widehat{ACE}=\widehat{MBC}=\widehat{ECB}\)

Xét ΔQBC có \(\widehat{QBC}=\widehat{QCB}\)

nên ΔQBC cân tại Q

=>QB=QC

Xét ΔAMB và ΔAEC có

\(\widehat{ABM}=\widehat{ACE}\)

AB=AC

\(\widehat{BAM}\) chung

Do đó: ΔAMB=ΔAEC

=>MB=EC

mà MB=MQ+QB

và EC=EQ+QC

và QB=QC

nên MQ=EQ

\(\dfrac{EG}{EB}+\dfrac{CI}{CM}=\dfrac{EQ}{EC}+\dfrac{BQ}{BM}=1-\dfrac{CQ}{CE}+\dfrac{BQ}{BM}\)

\(=1-\dfrac{BQ}{BM}+\dfrac{BQ}{BM}=1\)

a: Khi x=145 thì P=1496:(213-145)+237

=1496:68+237

=22+237=259

b: Đặt P=373

=>1496:(213-x)+237=373

=>1496:(213-x)=136

=>213-x=11

=>x=213-11=202

Khi x=145 thì P=1496:(213-145)+237

=1496:68+237

=22+237=259

 Đặt P=373

=>1496:(213-x)+237=373

=>1496:(213-x)=136

=>213-x=11

=>x=213-11=202