Tổng số cách chọn ra một bạn để phỏng vấn là: 1+5 = 6

Xác suất biến cố bạn nam được chọn là:

\(\left(1:6\right)=\dfrac{1}{6}\approx16,66\%\)

Đs...

Tổng số cách chọn ra một bạn để phỏng vấn là: 1+5 = 6

Xác suất biến cố bạn nam được chọn là:

(1:6)=16≈16,66%(1:6)=61​≈16,66%

a) Ta có:

A(x) + B(x) = (2x³ - x² + 3x - 5) + (2x³ + x² + x + 5)

                  = 4x³ + 4x

b) Ta có H(x) = A(x) + B(x) = 4x³ + 4x = 0

                                      => 4x(x² + 1) = 0

                                      => 4x = 0 hoặc x² + 1 = 0

                                      => x = 0 : 4 = 0 hoặc x² = 0 - 1 = -1 (vô lí)

Vậy nghiệm của H(x) = A(x) + B(x) là x = 0

a, A(x)+B(x)=4^3+4x

b,Vậy nghiệm của �(�)H(x) là �=0x=0.

Gọi số sách 2 lớp 7A và 7B lần lượt là a và b ( sách, a,b thuộc N*) 

Ta có a + b = 121 

Áp dụng tính chất dãy tỉ số bằng nhau ta có: 

a/5 = b/6 = a+b/ 5+6 = 121/11 = 11

Quyển sách lớp 7A quyên góp được là: 

11 x 5 = 55 

Số sách 7B quyên góp được là 

11 x 6 = 66 

Theo đề bài:

+) Lớp 7A và 7B quyên góp được 121121 quyển sách

Nên ta có: �+�=121x+y=121

+) Số sách giáo khoa của lớp 6A; lớp 6B tỉ lệ thuận với tỉ lệ thuận với 5; 6

Nên ta có: �5=�65x​=6y​

Áp dụng tính chất dãy tỉ số bằng nhau ta có �5=�6=�+�5+6=12111=115x​=6y​=5+6x+y​=11121​=11

Suy ra: x=55, y= 66 ( thỏa mãn).

Vậy lớp 6A quyên góp được 5555 quyển sách, lớp 6B quyên góp được 6666 cuốn.

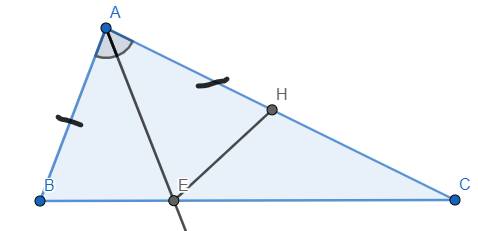
a) Xét ΔABE & ΔAHE có:

- AB = AH (giả thuyết); AE là cạnh chung; \(\widehat{BAE}=\widehat{HAE}\) (vì AE là tia phân giác góc BAC)

Suy ra ΔABE = ΔAHE (c.g.c)

Giúp mình với 

\(\dfrac{3x-2}{x-1}\) = - 3

3\(x\) - 2 = (\(x-1\)) \(\times\) ( -3) 

3\(x\) - 2 = -3\(x\) + 3

3\(x\) + 3\(x\) = 2 + 3

6\(x\) = 5

\(x\) = 5/6