x^2-2(m-2)x + m2 - 8 = 0
1/ tìm các giá trị tham số của m để phương trình đã cho có nghiệm bằng 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
Vì $BE, CF$ là đường cao của tam giác $ABC$ nên $\widehat{BFC}=\widehat{BEC}=90^0$
Tứ giác $BCEF$ có $\widehat{BFC}=\widehat{BEC}$ và cùng nhìn cạnh $BC$ nên $BCEF$ là tứ giác nội tiếp.
b.
Xét tam giác $BFH$ và $CFA$ có:
$\widehat{BFH}=\widehat{CFA}=90^0$
$\widehat{FBH}=\widehat{FBE}=\widehat{FCE}=\widehat{FCA}$ (do $BCEF$ là tgnt)
$\Rightarrow \triangle BFH\sim \triangle CFA$ (g.g)
$\Rightarrow \frac{BF}{CF}=\frac{BH}{CA}$
$\Rightarrow BF.CA=BH.CF$
c.
Kéo dài $AO$ cắt $(O)$ tại $M$ thì $O$ là trung điểm $AM$.
$K$ là trung điểm $BC$ nên $OK\perp BC$, AH\perp BC$ (do $H$ là trực tâm)
$\Rightarrow OK\parallel AH$
Có: $\widehat{ABM}=\widehat{ACM}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow AB\perp BM, AC\perp CM$
Mà $CH\perp AB, BH\perp AC$ nên $BM\parallel CH, CM\parallel BH$
$\Rightarrow BHCM$ là hình bình hành (tứ giác có 2 cặp cạnh đối song song)
$\Rightarrow HM, BC$ cắt nhau tại trung điểm $K$ của $BC$
$\Rightarrow H,K,M$ thẳng hàng.
Tam giác $AHM$, áp dụng định lý Talet có:
$\frac{OK}{AH}=\frac{OM}{AM}=\frac{1}{2}$

Lời giải:
Xét tứ giác $BFEC$ có: $\widehat{BFC}=\widehat{BEC}=90^0$ và cùng nhìn cạnh $BC$ nên $BFEC$ là tứ giác nội tiếp.
Kẻ tiếp tuyến $Ax$ của $(O)$. Theo tính chất tiếp tuyến thì $Ax\perp OA(1)$
Lại có:
Tứ giác $BFEC$ nội tiếp.
$\Rightarrow \widehat{BCE}=\widehat{AFE}$
Mà $\widehat{BCE}=\widehat{BCA}=\widehat{xAB}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn cung đó - cụ thể ở đây là cung $AB$)
$\Rightarrow \widehat{AFE}=\widehat{xAB}$
Mà 2 góc này ở vị trí so le trong nên $Ax\parallel EF(2)$
Từ $(1); (2)\Rightarrow EF\perp OA$

Bài 4:
a: \(\text{Δ}=\left(-m\right)^2-4\left(m-2\right)\)
\(=m^2-4m+8=\left(m-2\right)^2+4>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m\\x_1x_2=\dfrac{c}{a}=m-2\end{matrix}\right.\)
\(x_1-x_2=2\)
=>\(\left(x_1-x_2\right)^2=4\)
=>\(\left(x_1+x_2\right)^2-4x_1x_2=4\)
=>\(m^2-4\left(m-2\right)-4=0\)
=>\(m^2-4m+4=0\)
=>\(\left(m-2\right)^2=0\)
=>m-2=0
=>m=2
cho tam giác vuông ABC vuông tại A, biết AB=7 cm, BC=10 cm.
tính các tỉ số lượng giác của góc B và góc C

a: 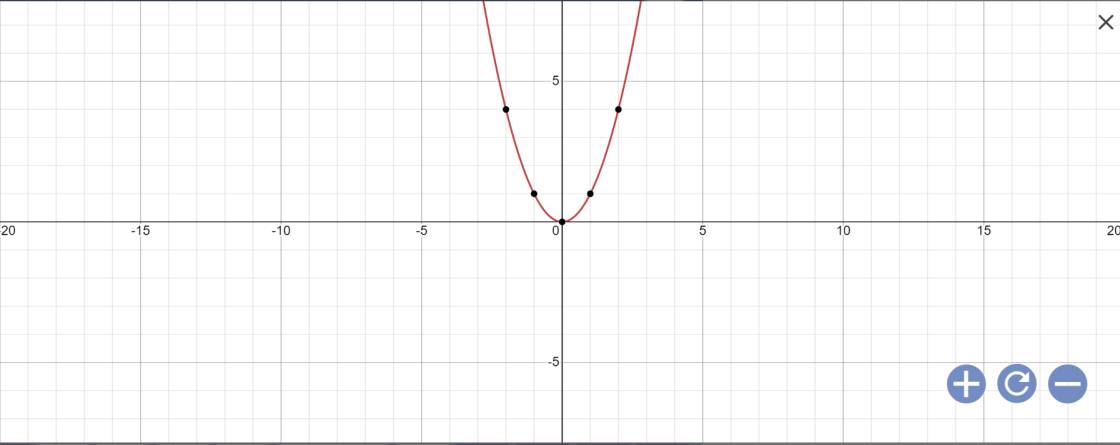
b: Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x+6\)
=>\(x^2-\left(m-2\right)x-6=0\)
\(a\cdot c=1\cdot\left(-6\right)=-6< 0\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m-2\\x_1x_2=\dfrac{c}{a}=-6\end{matrix}\right.\)
\(x_2^2-x_1x_2+\left(m-2\right)x_1=16\)
=>\(x_2^2+x_1\left(x_1+x_2\right)-x_1x_2=16\)
=>\(x_2^2+x_1^2=16\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=16\)
=>\(\left(m-2\right)^2-2\cdot\left(-6\right)=16\)
=>\(\left(m-2\right)^2=4\)
=>\(\left[{}\begin{matrix}m-2=2\\m-2=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=4\\m=0\end{matrix}\right.\)

ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn tâm O, đường kính BC
=>O là trung điểm của BC
Vì OA=OC
nên O nằm trên đường trung trực của AC
=>OD là đường trung trực của AC
=>OD\(\perp\)AC
mà AB\(\perp\)AC
nên OD//AB
=>\(\widehat{ODB}=\widehat{ABD}\)
mà \(\widehat{ABD}=\widehat{OBD}\)(BD là phân giác của góc ABC)
nên \(\widehat{OBD}=\widehat{ODB}\)
=>OB=OD=R
=>D thuộc đường tròn ngoại tiếp ΔABC


Gọi vận tốc xe đi từ A là: x(km/giờ) (ĐK:0<x<50)
vận tốc xe đi từ B là: y(km/giờ) (ĐK:0<y<50)
- Trong 5 giờ xe đi từ A và xe đi từ B lần lượt đi được: 5x và 5y (km)
Vì 2 xe đi ngược chiều nhau và gặp nhau sau 5 giờ, nên tổng quãng đường 2 xe đi được trong 5 giờ chính là quãng đường AB. Ta có pt:
5x+5y=250 <=> x+y=50 (1)
- Trong 1 giờ, xe đi từ A đi được: x (km)
- Trong 2 giờ, xe đi từ B đi được: 2y (km)
Mà xe đi từ A đi trong 1 giờ, xe đi từ B đi trong 2 giờ thì chúng cách nhau 70km hay quãng đường 2 xe đi được là 180km nên ta có pt:
x+2y=180(2)
(1) và (2) ta có hpt: \(\left\{{}\begin{matrix}x+y=50\\x+2y=180\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=130\\x=50-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=130\\x=-80\end{matrix}\right.\left(loại\right)\)
Mình nghĩ bạn có sai sót đề ở đây
Mình sửa lại nhé: Sau khi 2 xe gặp nhau, xe đi từ A đi tiếp trong 1 giờ rồi dừng và xe đi từ B đi tiếp trong 2 giờ rồi dừng lúc này 2 xe cách nhau 70km
Vẫn lập luận như cũ nhưng khác ở pt 2 nhé bạn
Mà sau khi gặp nhau xe đi từ A đi tiếp 1 giờ và xe đi từ B đi tiếp trong 2 giờ thì 2 xe cách nhau 70km hay tổng quãng đường 2 xe đi được trong thời gian này là 70km nên ta có pt:
x+2y=70(2)
(1);(2) ta có hpt: \(\left\{{}\begin{matrix}x+y=50\\x+2y=70\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=20\\x=50-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=20\\x=30\end{matrix}\right.\left(TM\right)\)
Vậy vận tốc xe đi từ A là: 30km/giờ và vận tốc xe đi từ B là: 20km/giờ
1: Thay x=2 vào phương trình, ta được:
\(2^2-2\left(m-2\right)\cdot2+m^2-8=0\)
=>\(4-4\left(m-2\right)+m^2-8=0\)
=>\(4-4m+8+m^2-8=0\)
=>\(m^2-4m+4=0\)
=>\(\left(m-2\right)^2=0\)
=>m-2=0
=>m=2