Có 5292 lạng bạc phát cho 328 người, chia làm ba hạng: hạng Giáp 8 người, mỗi người được 7 phần; hạng Ất 20 người, mỗi người 5 phần; hạng Bính 300 người, mỗi người được 2 phần. Hỏi mỗi người ở mỗi hạng được lĩnh bao nhiêu lạng lạc.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`(x-2):(x-1)=(x+4)(x+7)`
\(< =>\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\left(x\ne1;x\ne-7\right)\)
`=>(x-2)(x+7)=(x+4)(x-1)`
`<=>x^2 +7x-2x-14=x^2 -x+4x-4`
`<=>x^2 +5x-14-x^2 -3x+4=0`
`<=>2x-10=0`
`<=>2x=10`
`<=>x=5(tm)`


\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
\(=\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+\dfrac{1}{4\times5}+\dfrac{1}{5\times6}+\dfrac{1}{6\times7}+\dfrac{1}{7\times8}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
\(=\dfrac{1}{2}-\dfrac{1}{8}=\dfrac{8}{16}-\dfrac{2}{16}\)
\(=\dfrac{6}{16}=\dfrac{3}{8}\)

Gọi N là giao điểm của BM và AC. Do \(\widehat{NAM}=\widehat{NBA}\) nên \(\Delta NAM\) đồng dạng với \(\Delta NBA\), suy ra \(\dfrac{NA}{NB}=\dfrac{NM}{NA}\) \(\Rightarrow NA^2=NB.NM\) (1)
Mặt khác, vì tam giác ABC vuông cân tại A nên \(\widehat{ABC}=\widehat{ACB}=45^o\), lại có \(\widehat{MBA}=\widehat{MCA}\) nên ta có \(\widehat{ABC}-\widehat{MBA}=\widehat{ACB}-\widehat{MCA}\) hay \(\widehat{NBC}=\widehat{NCM}\). Từ đây có\(\Delta NCM\) đồng dạng với tam giác \(\Delta NBC\), suy ra \(\dfrac{NC}{NB}=\dfrac{NM}{NC}\Rightarrow NC^2=NB.NM\) (2)
Từ (1) và (2), suy ra \(NA^2=NC^2\left(=NB.NM\right)\) \(\Rightarrow NA=NC\), suy ra N là trung điểm của đoạn AC \(\Rightarrow\dfrac{AN}{AC}=\dfrac{1}{2}\). Mà \(AC=AB\) nên \(\dfrac{AN}{AB}=\dfrac{1}{2}\)
Mặt khác, \(\widehat{BAC}=\widehat{MAN}+\widehat{BAM}=90^o\), đồng thời \(\widehat{MAN}=\widehat{MBA}\) nên \(\widehat{MBA}+\widehat{BAM}=90^o\), do đó \(\Delta ABM\) vuông tại M \(\Rightarrow\widehat{AMB}=90^o\). Từ đó lại suy ra \(\Delta BAM\) và \(\Delta BNA\) đồng dạng, suy ra \(\dfrac{AN}{AM}=\dfrac{BA}{BM}\) hay \(\dfrac{AN}{AB}=\dfrac{AM}{BM}\). Nhưng do \(\dfrac{AN}{AB}=\dfrac{1}{2}\left(cmt\right)\) nên \(\dfrac{AM}{BM}=\dfrac{1}{2}\Rightarrow BM=2AM\) (đpcm)

`4/3 +11/6 -2/9 - 5/3`
`= (4/3 - 5/3)+11/6-2/9`
`= -1/3 +11/6 -2/9`
`= -2/6 +11/6 -2/9`
`= 9/6 -2/9`
`= 3/2 -2/9`
`= 27/18 - 4/18`
`= 23/18`
`@` `\text {Ans}`
`\downarrow`
\(\dfrac{4}{3}+\dfrac{11}{6}-\dfrac{2}{9}-\dfrac{5}{3}\)
`=`\(\left(\dfrac{11}{6}-\dfrac{2}{9}\right)+\left(\dfrac{4}{3}-\dfrac{5}{3}\right)\)
`=`\(\dfrac{29}{18}-\dfrac{1}{3}=\dfrac{23}{18}\)
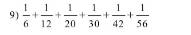
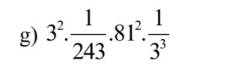
Gọi số lạng bạc của mỗi phần là: \(x\) (\(x\) > 0) (lạng)
Số bạc của 8 người hạng giáp là: \(x\) \(\times\) 7 \(\times\) 8 = 56\(x\) (lạng)
Số bạc của 20 người hạng Ất là: \(x\times\)5\(\times\)20 = 100\(x\) (lạng)
Số bạc của 300 người hạng Bính là: \(x\times\)2\(\times\)300 = 600\(x\) (lạng)
Theo bài ra ta có: 56\(x\) + 100\(x\)+ 600\(x\) = 5292
756\(x\) = 5292
\(x\) = 7
Vậy mỗi phần có số lạng bạc là : 7 lạng
Số lạng bạc mà mỗi người hạng Giáp nhận được là:
7 \(\times\) 7 = 49 (lạng)
Số lạng bạc mà mỗi người hạng Ất nhận được là:
7 \(\times\) 5 = 35 (lạng)
Số lạng bạc mà mỗi người hạng Bính nhận được là:
7 \(\times\) 2 = 14 (lạng)
Kết luận: Mỗi người hạng Giáp nhận được 49 lạng bạc
Mỗi người hạng Ất nhận được 35 lạng bạc
Mỗi người hạng Bính nhận được 14 lạng bạc