Một bể bơi hình hộp chữ nhật dài 25m, rộng 12m và sâu 2,5m. Người ta lát mặt xung quanh bể và mặt đáy bằng gạch men hình vuông có cạnh 50cm. Số viên gạch cần có là:
* A. 1570 B. 740 C. 3140 D. 1940giHãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{x-1}\)
\(=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(2\sqrt{x}-3\right)\left(\sqrt{x}+1\right)+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x+2\sqrt{x}-3\sqrt{x}-3+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\)

`300 + 600 + 400 + 700 + 545 + 455`
`= (300 + 700) + (600 + 400) + (545 + 455)`
`= 1000 + 1000 + 1000`
`=3000`

Câu 1: B
Câu 2: C
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: B
Câu 7: D
Câu 8: A
Câu 9: D
Câu 10: D

\(B=\dfrac{2x-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{x-1}\)
\(=\dfrac{2x-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(2x-3\right)\left(\sqrt{x}+1\right)+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x\sqrt{x}+2x-3\sqrt{x}-3+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x\sqrt{x}+2x-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}+1}=\dfrac{2x+4\sqrt{x}}{\sqrt{x}+1}\)

a: \(\text{Δ}=\left(-3\right)^2-4\left(-m^2+2\right)\)
\(=9+4m^2-8=4m^2+1>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
b:
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=3\\x_1x_2=\dfrac{c}{a}=-m^2+2\end{matrix}\right.\)
\(x_1>x_2\)
=>\(x_1-x_2>0\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=3^2-4\left(-m^2+2\right)\)
\(=9+4m^2-8=4m^2+1\)
=>\(x_1-x_2=\sqrt{4m^2+1}\)
\(A=x_1^2-x_2^2+5\left(x_1+x_2\right)\)
\(=\left(x_1-x_2\right)\left(x_1+x_2\right)+5\left(x_1+x_2\right)\)
\(=3\sqrt{4m^2+1}+15>=3\cdot1+15=18\forall m\)
Dấu '=' xảy ra khi m=0

Câu 1: B
Câu 2: C
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: B
Câu 7: D
Câu 8: A
Câu 9: D
Câu 10: D

Tổng của năm số:
30 × 5 = 150
Số thứ năm là:
150 - (10 + 20 + 30 + 50) = 40

Lời giải:
Trong 1 giờ vòi thứ nhất chảy được $\frac{1}{2}$ (bể)
Vì vòi thứ hai có sức chảy bằng vòi thứ nhất nên sau 1 giờ vòi 2 cũng chảy được $\frac{1}{2}$ bể
Trong 1 giờ cả hai vòi chảy được: $\frac{1}{2}+\frac{1}{2}=1$ (bể)
Vậy trong 1 giờ 2 vòi cùng chảy sẽ đầy bể.
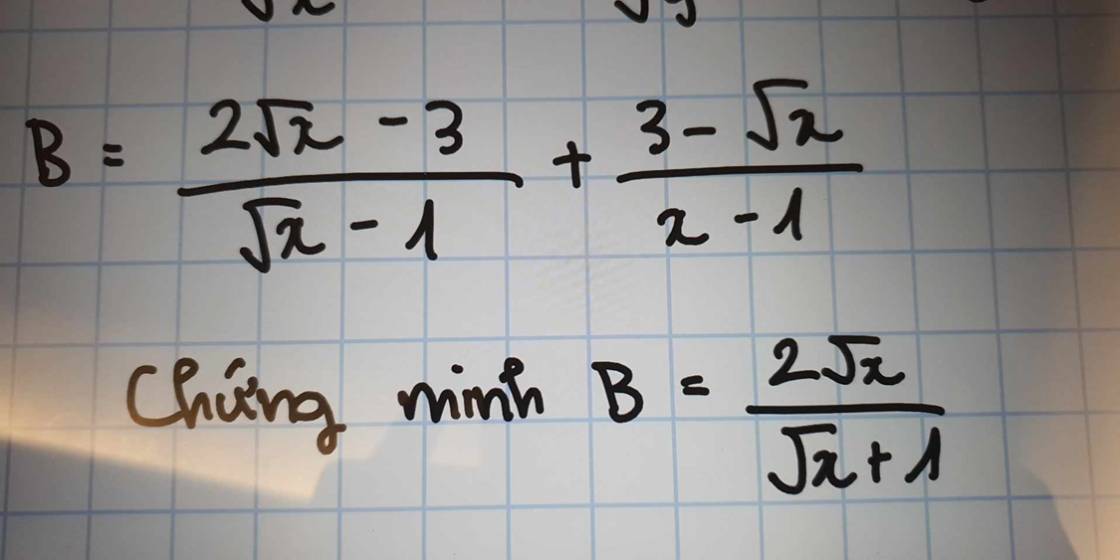

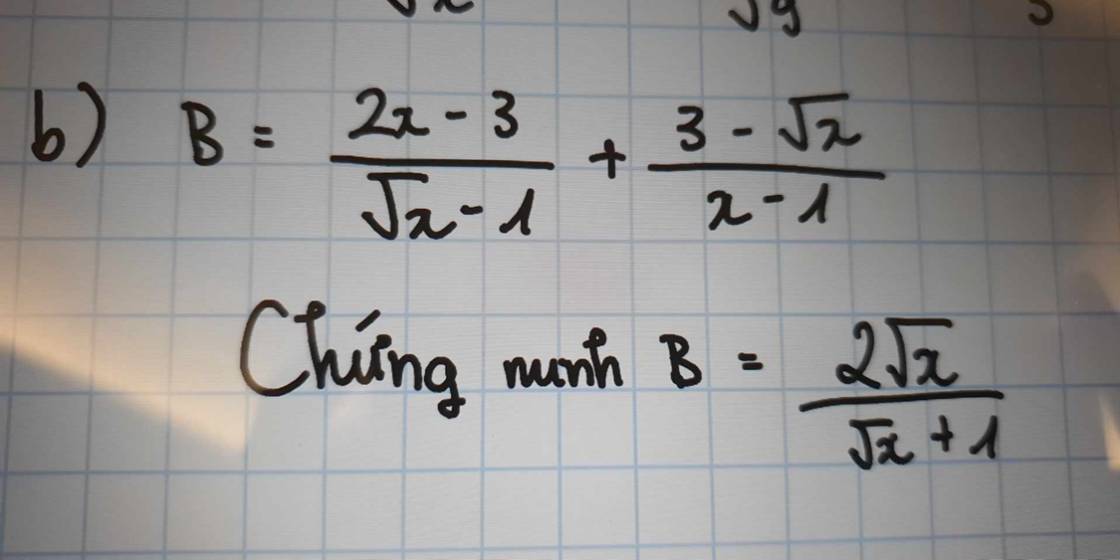 Bạn nào biết giải bài này không ạ giúp mình nhé. Mình cảm ơn nhiều
Bạn nào biết giải bài này không ạ giúp mình nhé. Mình cảm ơn nhiều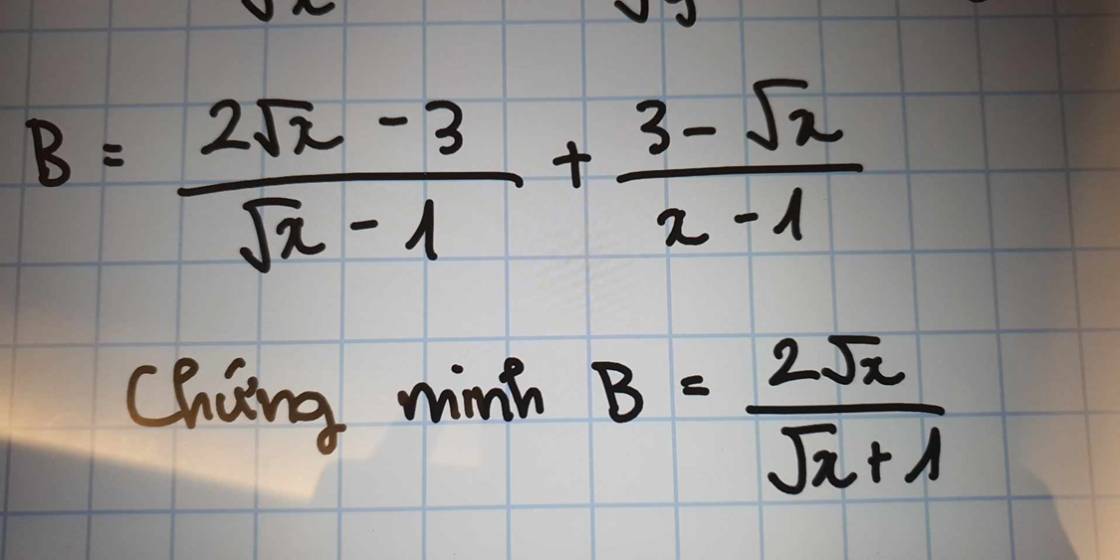
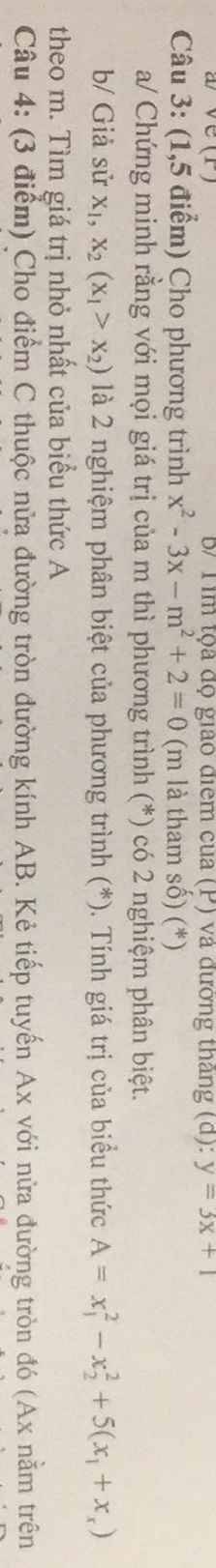

Diện tích xung quanh là:
\(\left(25+12\right)\cdot2\cdot2,5=5\cdot37=185\left(m^2\right)\)
Diện tích cần lát gạch là:
\(185+25\cdot12=185+300=485\left(m^2\right)\)=4850000(cm2)
Diện tích 1 viên gạch là 502=2500(cm2)
Số viên gạch cần dùng là:
4850000:2500=1940(viên)
=>Chọn D
50 cm = 0.5 m
Diện tích xung quanh bể bơi :
( 25 + 12 ) . 2.5 . 2 = 185 ( m2 )
Diện tích đáy bể :
25 . 12 = 300 ( m2 )
Diện tích cần lát gạch :
185 + 300 = 485 ( m2 )
Số gạch cần để lát :
485 : ( 0.5 . 0.5 ) = 1940 ( viên )