Cho ba số thực dương x, y, z thỏa mãn x * y ^ 2 + y * z ^ 2 + z * x ^ 2 = 3xyz Tìm giá trị nhỏ nhất của biểu thức P = (x * z ^ 2)/(y(y ^ 2 + z ^ 2)) + (y * x ^ 2)/(z(z ^ 2 + x ^ 2)) + (z * y ^ 2)/(x(x ^ 2 + y ^ 2))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+b^2d^2+2acbd+a^2d^2+b^2c^2-2adbc\)
\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)
b: \(x^2+y^2=\dfrac{1}{2}\left(2x^2+2y^2\right)\)
\(=\dfrac{1}{2}\left(x^2+2xy+y^2+x^2-2xy+y^2\right)\)
\(=\dfrac{1}{2}\left[\left(x+y\right)^2+\left(x-y\right)^2\right]=\dfrac{1}{2}\left[4+\left(x-y\right)^2\right]>=\dfrac{1}{2}\cdot4=2\)
Dấu '=' xảy ra khi x=y=1

1: Thay x=2 vào phương trình, ta được:
\(2^2-2\left(m-2\right)\cdot2+m^2-8=0\)
=>\(4-4\left(m-2\right)+m^2-8=0\)
=>\(4-4m+8+m^2-8=0\)
=>\(m^2-4m+4=0\)
=>\(\left(m-2\right)^2=0\)
=>m-2=0
=>m=2

Lời giải:
a.
Vì $BE, CF$ là đường cao của tam giác $ABC$ nên $\widehat{BFC}=\widehat{BEC}=90^0$
Tứ giác $BCEF$ có $\widehat{BFC}=\widehat{BEC}$ và cùng nhìn cạnh $BC$ nên $BCEF$ là tứ giác nội tiếp.
b.
Xét tam giác $BFH$ và $CFA$ có:
$\widehat{BFH}=\widehat{CFA}=90^0$
$\widehat{FBH}=\widehat{FBE}=\widehat{FCE}=\widehat{FCA}$ (do $BCEF$ là tgnt)
$\Rightarrow \triangle BFH\sim \triangle CFA$ (g.g)
$\Rightarrow \frac{BF}{CF}=\frac{BH}{CA}$
$\Rightarrow BF.CA=BH.CF$
c.
Kéo dài $AO$ cắt $(O)$ tại $M$ thì $O$ là trung điểm $AM$.
$K$ là trung điểm $BC$ nên $OK\perp BC$, AH\perp BC$ (do $H$ là trực tâm)
$\Rightarrow OK\parallel AH$
Có: $\widehat{ABM}=\widehat{ACM}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow AB\perp BM, AC\perp CM$
Mà $CH\perp AB, BH\perp AC$ nên $BM\parallel CH, CM\parallel BH$
$\Rightarrow BHCM$ là hình bình hành (tứ giác có 2 cặp cạnh đối song song)
$\Rightarrow HM, BC$ cắt nhau tại trung điểm $K$ của $BC$
$\Rightarrow H,K,M$ thẳng hàng.
Tam giác $AHM$, áp dụng định lý Talet có:
$\frac{OK}{AH}=\frac{OM}{AM}=\frac{1}{2}$

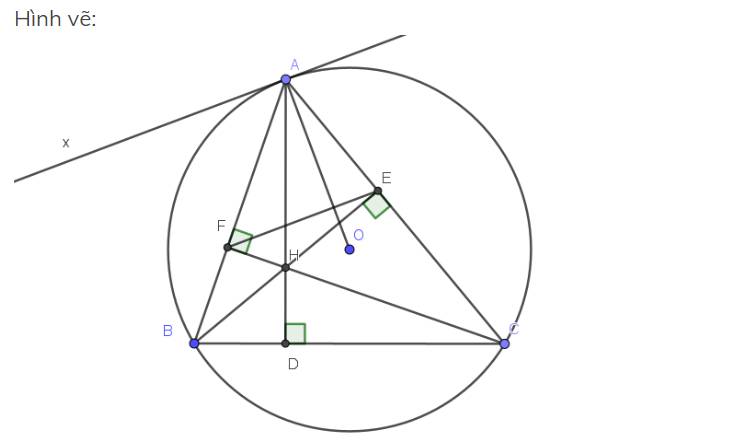
Lời giải:
Xét tứ giác $BFEC$ có: $\widehat{BFC}=\widehat{BEC}=90^0$ và cùng nhìn cạnh $BC$ nên $BFEC$ là tứ giác nội tiếp.
Kẻ tiếp tuyến $Ax$ của $(O)$. Theo tính chất tiếp tuyến thì $Ax\perp OA(1)$
Lại có:
Tứ giác $BFEC$ nội tiếp.
$\Rightarrow \widehat{BCE}=\widehat{AFE}$
Mà $\widehat{BCE}=\widehat{BCA}=\widehat{xAB}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn cung đó - cụ thể ở đây là cung $AB$)
$\Rightarrow \widehat{AFE}=\widehat{xAB}$
Mà 2 góc này ở vị trí so le trong nên $Ax\parallel EF(2)$
Từ $(1); (2)\Rightarrow EF\perp OA$

Bài 4:
a: \(\text{Δ}=\left(-m\right)^2-4\left(m-2\right)\)
\(=m^2-4m+8=\left(m-2\right)^2+4>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m\\x_1x_2=\dfrac{c}{a}=m-2\end{matrix}\right.\)
\(x_1-x_2=2\)
=>\(\left(x_1-x_2\right)^2=4\)
=>\(\left(x_1+x_2\right)^2-4x_1x_2=4\)
=>\(m^2-4\left(m-2\right)-4=0\)
=>\(m^2-4m+4=0\)
=>\(\left(m-2\right)^2=0\)
=>m-2=0
=>m=2
cho tam giác vuông ABC vuông tại A, biết AB=7 cm, BC=10 cm.
tính các tỉ số lượng giác của góc B và góc C

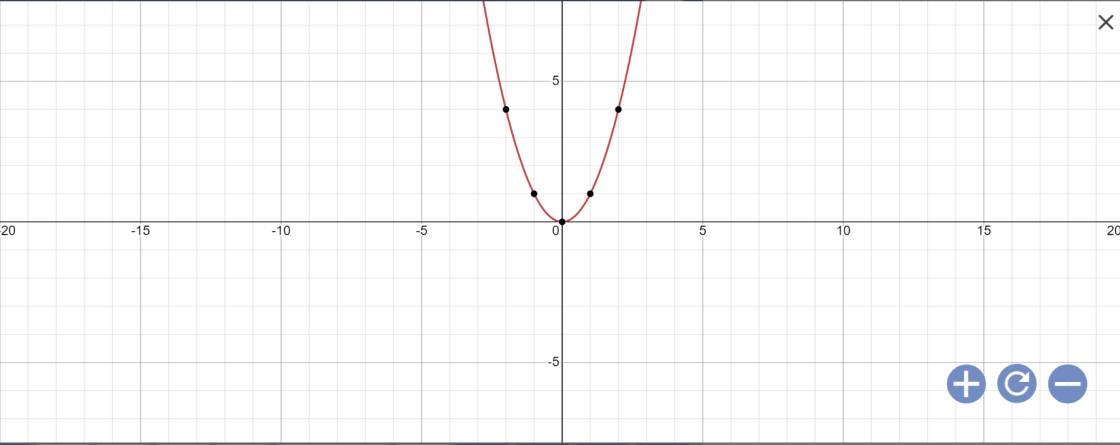
a: 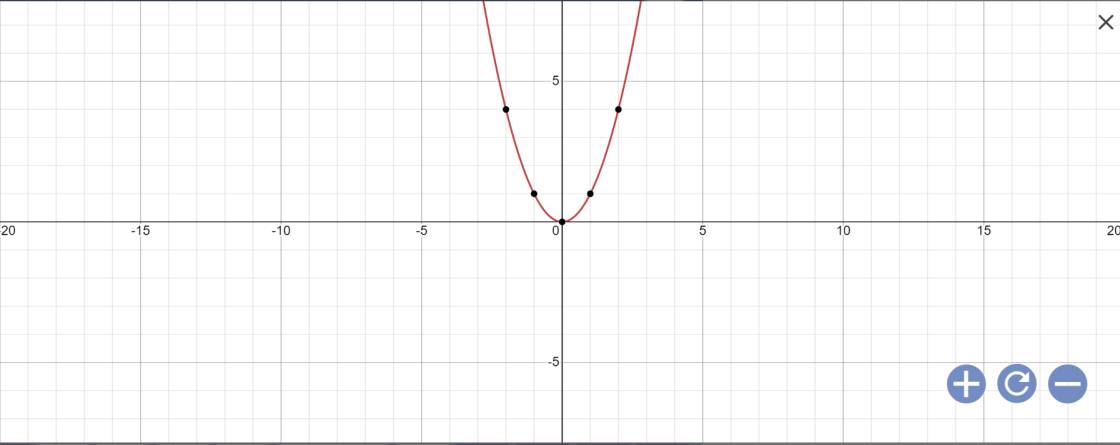
b: Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x+6\)
=>\(x^2-\left(m-2\right)x-6=0\)
\(a\cdot c=1\cdot\left(-6\right)=-6< 0\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m-2\\x_1x_2=\dfrac{c}{a}=-6\end{matrix}\right.\)
\(x_2^2-x_1x_2+\left(m-2\right)x_1=16\)
=>\(x_2^2+x_1\left(x_1+x_2\right)-x_1x_2=16\)
=>\(x_2^2+x_1^2=16\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=16\)
=>\(\left(m-2\right)^2-2\cdot\left(-6\right)=16\)
=>\(\left(m-2\right)^2=4\)
=>\(\left[{}\begin{matrix}m-2=2\\m-2=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=4\\m=0\end{matrix}\right.\)


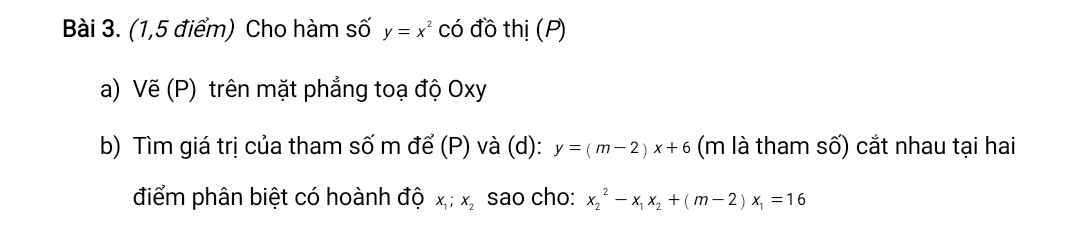

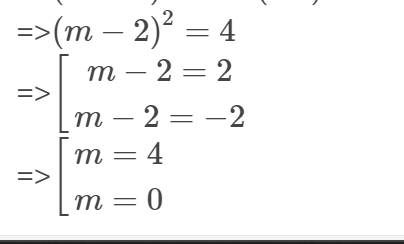
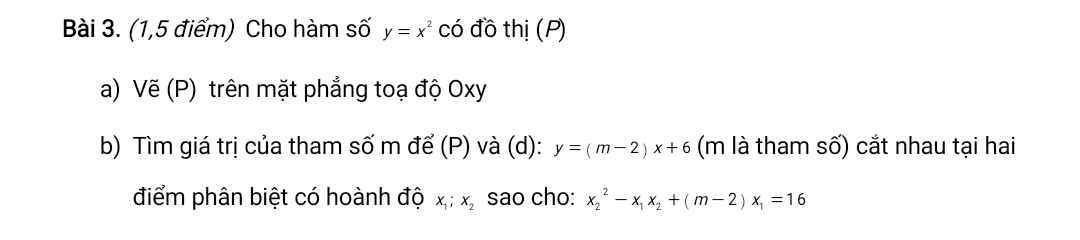
x2+y2+z2=3xyz⇒xyz+yxz+zxy=3�2+�2+�2=3���⇒���+���+���=3
Áp dụng bất đẳng thức Cô-si cho hai số dương xyz;yxz���;��� ta có: xyz+yxz≥2√xyz.yx=2z���+���≥2���.��=2�
Tương tự ta cũng có: yxz+zxy≥2x;zxy+xyz≥2y���+���≥2�; ���+���≥2�
⇒(xyz+yxz)+(yxz+zxy)+(zxy+xyz)≥2z+2x+2y⇒xyz+yzx+zxy≥1x+1y+1z⇒1x+1y+1z≤3⇒���+���+���+���+���+���≥2�+2�+2�⇒���+���+���≥1�+1�+1�⇒1�+1�+1�≤3
Lại có: x4+yz≥2√x4yz=2x2√yz⇒x2x4+yz≤12√yz=14.2.1√y.1√z≤14(1y+1z)�4+��≥2�4��=2�2��⇒�2�4+��≤12��=14.2.1�.1�≤14(1�+1�)
Tương tự y2y4+xz≤14(1x+1z);z2z4+xy≤14(1x+1y)�2�4+��≤14(1�+1�);�2�4+��≤14(1�+1�)
Suy ra
P=x2x4+yz+y2y4+xz+z2z4+xy≤14(2x+2y+2z)=12(1x+1y+1z)≤32=>P≤32�=�2�4+��+�2�4+��+�2�4+��≤14(2�+2�+2�)=12(1�+1�+1�)≤32=>�≤32
Vậy giá trị nhỏ nhất của P = 3232 khi x = y = z = 1.