3x +60 = -120 giúp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`#3107.101107`
`(2x + 1)^3 = 343`
`\Rightarrow (2x + 1)^3 = 7^3`
`\Rightarrow 2x + 1 = 7`
`\Rightarrow 2x = 6`
`\Rightarrow x = 3`
Vậy, `x = 3.`

B = \(\dfrac{4}{7}\) = \(\dfrac{4.4}{7.4}\) = \(\dfrac{16}{28}\); I = \(\dfrac{6}{13}\) = \(\dfrac{6.\left(-2\right)}{13.\left(-2\right)}\) = \(\dfrac{-12}{-26}\)
N = \(\dfrac{-5}{13}\) = \(\dfrac{-5.3}{13.3}\) = \(\dfrac{-15}{39}\); T = \(\dfrac{7}{21}\) = \(\dfrac{7.4}{21.4}\) = \(\dfrac{28}{84}\)
U = \(\dfrac{4}{11}\) = \(\dfrac{4.5}{11.5}\) = \(\dfrac{20}{55}\); O = \(\dfrac{5}{25}\) = \(\dfrac{5.3}{25.3}\) = \(\dfrac{15}{75}\)
H = \(\dfrac{1}{5}\) = \(\dfrac{1.11}{5.11}\) = \(\dfrac{11}{15}\); A = \(\dfrac{5}{8}\) = \(\dfrac{5.5}{8.5}\) = \(\dfrac{25}{40}\)
G = \(\dfrac{-3}{17}\) = \(\dfrac{-3.5}{17.5}\) = \(\dfrac{-15}{85}\); D = \(\dfrac{4}{16}\) = \(\dfrac{4.5}{16.5}\) = \(\dfrac{20}{80}\)
| T | H | A | I | B | I | N | H | D | U | O | N | G |
| 84 | 11 | 25 | -12 | 16 | -12 | -15 | 11 | 80 | 55 | 75 | -15 | 85 |

B. $\frac{4}{7}=\frac{16}{28}$
N. $\frac{-5}{13}=\frac{-15}{39}$
U. $\frac{4}{11}=\frac{20}{55}$
H. $\frac{1}{5}=\frac{11}{55}$
G. $\frac{-3}{17}=\frac{-15}{85}$
I. $\frac{6}{13}=\frac{-12}{-26}$
T. $\frac{7}{21}=\frac{28}{84}$
O. $\frac{5}{25}=\frac{15}{75}$
A. $\frac{5}{8}=\frac{25}{40}$
D. $\frac{4}{16}=\frac{20}{80}$

Ta có: \(xy-2x+3y=-5\)
\(\Rightarrow\left(xy-2x\right)+3y-6=-5-6\)
\(\Rightarrow x\left(y-2\right)+3\left(y-2\right)=-11\)
\(\Rightarrow\left(x+3\right)\left(y-2\right)=-11\)
Vì \(x,y\) nguyên nên \(x+3;y-2\) có giá trị nguyên
\(\Rightarrow x+3;y-2\) là các ước của \(-11\)
Ta có bảng sau:
| x + 3 | 1 | 11 | -1 | -11 |
| y - 2 | -11 | -1 | 11 | 1 |
| x | -2 | 8 | -4 | -14 |
| y | -9 | 1 | 13 | 3 |
Vì \(x,y\) nguyên nên ta được các cặp giá trị \(\left(x;y\right)\) là:
\(\left(-2;-9\right);\left(8;1\right);\left(-4;13\right);\left(14;3\right)\)
\(Toru\)

a) Ta có: \(\left|x+5\right|\ge0\forall x\)
\(\Rightarrow\left|x+5\right|+2023\ge2023\forall x\)
\(\Rightarrow A\ge2023\forall x\)
Dấu \("="\) xảy ra khi: \(x+5=0\Leftrightarrow x=-5\)
Vậy \(Min_A=2023\) khi \(x=-5\).
b) Ta có: \(\left\{{}\begin{matrix}\left|2x+6\right|\ge0\forall x\\\left|y+3x\right|\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left|2x+6\right|+\left|y+3x\right|\ge0\forall x,y\)
\(\Rightarrow\left|2x+6\right|+\left|y+3x\right|+25\ge25\forall x,y\)
\(\Rightarrow B\ge25\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}2x+6=0\\y+3x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-6\\y=-3x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-6:2=-3\\y=-3\cdot\left(-3\right)=9\end{matrix}\right.\)
Vậy \(Min_B=25\) khi \(x=-3;y=9\).
c) Ta có: \(\left\{{}\begin{matrix}\left|12-3x\right|\ge0\forall x\\\left|-y-4x\right|\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left|12-3x\right|+\left|-y-4x\right|\ge0\forall x,y\)
\(\Rightarrow\left|12-3x\right|+\left|-y-4x\right|-12\ge-12\forall x,y\)
\(\Rightarrow C\ge-12\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}12-3x=0\\-y-4x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=12\\y=-4x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=12:3=4\\y=-4\cdot4=-16\end{matrix}\right.\)
Vậy \(Min_C=-12\) khi \(x=4;y=-16\).
\(\mathit{Toru}\)

Theo đề bài,ta có:
\(49⋮x;56⋮x\) và \(x\) lớn nhất \(\Rightarrow x\inƯCLN\left(49;56\right)=7\)
Vậy \(x=7\)

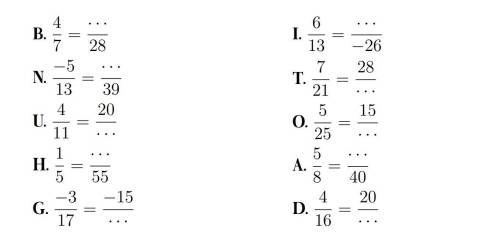
\(3x+60=-120\)
\(3x=-120-60\)
\(3x=-180\)
\(x=-180\div3\)
\(x=-60\)
\(3x+60=-120\\ \Rightarrow3x=-180\\ \Rightarrow x=-60.\)
Vậy ....