\(C_{BHKC}=96\)

=>\(4\times BH=96\)

=>BH=24(cm)

=>AD=BC=24(cm)

\(S_{MNPQ}=QN\times\dfrac{MP}{2}=AB\times\dfrac{BC}{2}\)

mà \(S_{MNPQ}=576\left(cm^2\right)\)

nên \(AB\times\dfrac{24}{2}=576\)

=>AB=576:12=48(cm)

AH=AB+BH=48+24=72(cm)

=>\(C_{AHKD}=\left(AH+AD\right)\times2=\left(72+24\right)\times2=192\left(cm\right)\)

=>Chọn A

Tổng số HS 3 lớp 5A, 5B và 5C nhiều hơn số HS lớp 5B là 75HS

hay tổng số HS lớp 5A và 5C là 75 HS

Theo đề, coi số HS lớp 5A là 7 phần và số HS lớp 5C là 8 phần

Tổng số phần bằng nhau:

 7+8=15 (phần)

Số HS lớp 5A là:

 75:15x7=35 (HS)

Số HS lớp 5C là:

 75-35=40(HS)

Đề chưa rõ dữ kiện để có thể xác định được số HS lớp 5B nhé bạn.

1000 học sinh

học sinh nữ:500

học sinh nam:500

1000-500=500                               500+500=1000

137,69-16,4x3,5+7,3:0,5

=137,69-57,4+14,6

=94,89

\(\dfrac{21-x}{29-x}=\dfrac{7}{11}\)

=>\(\dfrac{x-21}{x-29}=\dfrac{7}{11}\)

=>\(11\times\left(x-21\right)=7\times\left(x-29\right)\)

=>\(11x-231=7x-203\)

=>\(11x-7x=-203+231\)

=>4x=28

=>x=7

a: Để A là số nguyên thì \(n-5⋮n+1\)

=>\(n+1-6⋮n+1\)

=>\(-6⋮n+1\)

=>\(n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)

=>\(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)

Khi n=0 thì \(A=\dfrac{0-5}{0+1}=-5< 0\)(nhận)

Khi n=-2 thì \(A=\dfrac{-2-5}{-2+1}=\dfrac{-7}{-1}=7>0\left(loại\right)\)

Khi n=1 thì \(A=\dfrac{1-5}{1+1}=\dfrac{-4}{2}=-2< 0\)(nhận)

Khi n=-3 thì \(A=\dfrac{-3-5}{-3+1}=\dfrac{-8}{-2}=4>0\)(loại)

Khi n=2 thì \(A=\dfrac{2-5}{2+1}=\dfrac{-3}{3}=-1< 0\)(nhận)

Khi n=-4 thì \(A=\dfrac{-4-5}{-4+1}=\dfrac{-9}{-3}=3>0\left(loại\right)\)

Khi n=5 thì \(A=\dfrac{5-5}{5+1}=0\left(loại\right)\)

Khi n=-7 thì \(A=\dfrac{-7-5}{-7+1}=\dfrac{-12}{-6}=2>0\left(loại\right)\)

b: \(A=\dfrac{n-5}{n+1}=\dfrac{n+1-6}{n+1}=1-\dfrac{6}{n+1}\)

Để A có giá trị nhỏ nhất thì \(-\dfrac{6}{n+1}\) nhỏ nhất

=>\(\dfrac{6}{n+1}\) lớn nhất

=>n+1=1

=>n=0

Để A có giá trị lớn nhất thì \(\dfrac{6}{n+1}\) nhỏ nhất

=>n+1=-1

=>n=-2

\(\dfrac{64\text{x}50+44+100}{27\text{x}38+146\text{x}19}\)

\(=\dfrac{3200+144}{19\text{x}\left(27\text{x}2+146\right)}=\dfrac{3344}{19\text{x}200}\)

\(=\dfrac{3344}{3800}=\dfrac{22}{25}\)

\(\left(1-\dfrac{1}{2}\right)\times\left(1-\dfrac{1}{3}\right)\times\left(1-\dfrac{1}{4}\right)\times...\times\left(1-\dfrac{1}{2006}\right)\times\left(1-\dfrac{1}{2007}\right)\\ =\dfrac{1}{2}\times\dfrac{2}{3}\times\dfrac{3}{4}\times...\times\dfrac{2005}{2006}\times\dfrac{2006}{2007}\\ =\dfrac{1}{2007}\)

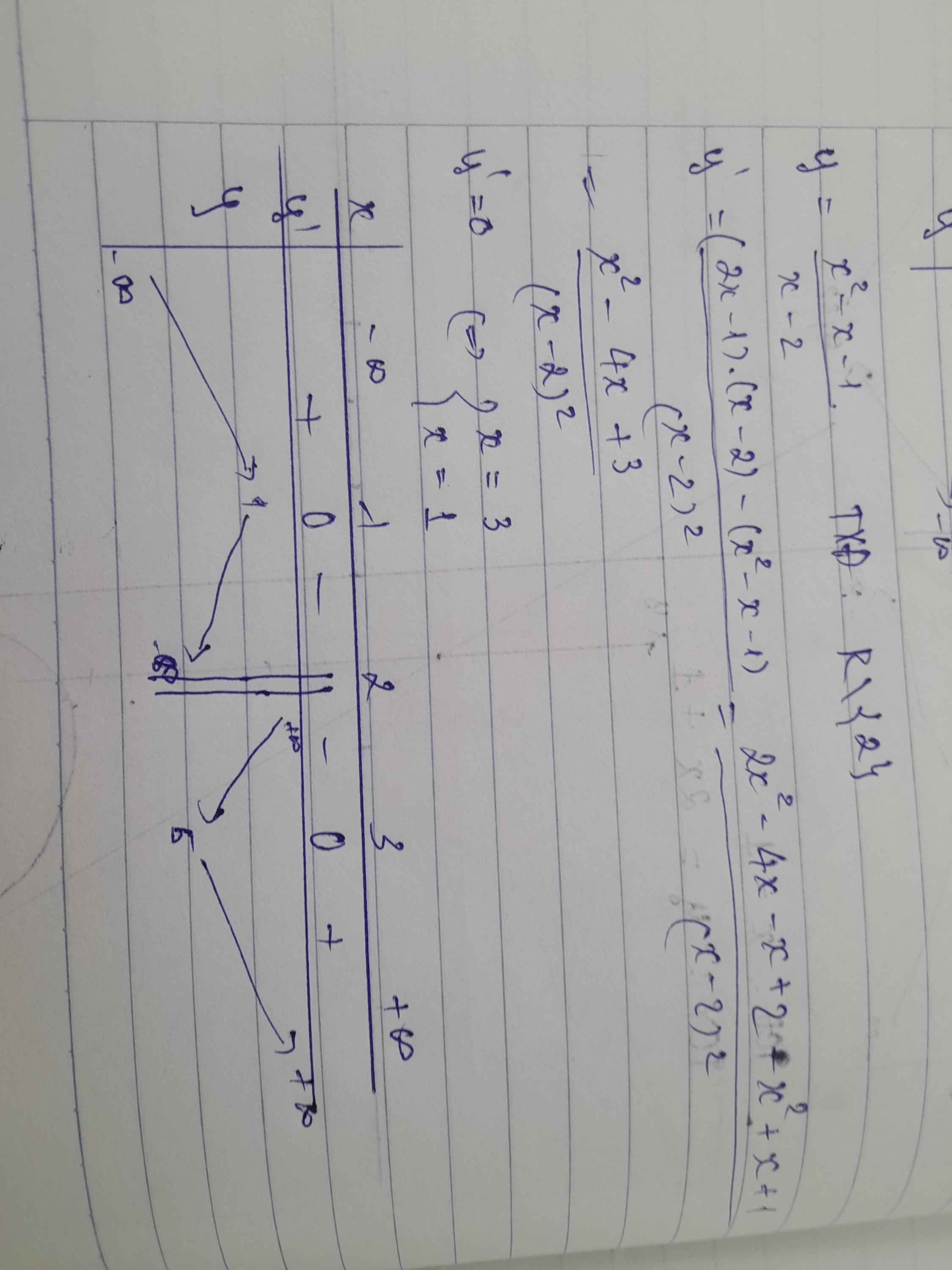
Tập xác định \(D=ℝ\backslash\left\{2\right\}\)

TCĐ: \(x=2\)

Có \(\dfrac{x^2-x-1}{x-2}=\dfrac{x^2-x-2+1}{x-2}=\dfrac{\left(x+1\right)\left(x-2\right)+1}{x-2}=\left(x+1\right)+\dfrac{1}{x-2}\)

nên đồ thị hàm số có tiệm cận xiên là đường \(y=x+1\)

Có \(y'=\dfrac{x^2-4x+3}{\left(x-2\right)^2}\)

\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

BBT

a: Số báo còn lại trong thư viện chiếm:

\(1-\dfrac{3}{5}=\dfrac{2}{5}\)(tổng số báo)

Số truyện còn lại trong thư viện chiếm:

\(1-\dfrac{2}{7}=\dfrac{5}{7}\)(tổng số truyện)

b: Số truyện còn lại là:

\(30:\left(1,5-1\right)\times1,5=30:0,5\times1,5=90\left(quyển\right)\)

Số báo còn lại là:

90:1,5=60(quyển)

Số truyện ban đầu là \(90:\dfrac{5}{7}=90\times\dfrac{7}{5}=126\left(quyển\right)\)

Số báo ban đầu là \(60:\dfrac{2}{5}=150\left(quyển\right)\)

Tổng số báo và truyện là:

150+126=276(quyển)