\(\left\{{}\begin{matrix}2x+y=3\\3x+2y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2.(2x+y)=3.2\\3x+2y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}4x+2y=6\\3x+2y=4\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}4x+2y-3x-2y=6-4\\3x+2y=4\end{matrix}\right.\)  ⇒ \(\left\{{}\begin{matrix}x=2\\3x+2y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=2\\3.2+2y=4\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=2\\2y=-2\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)

Vậy (\(x;y\)) =( 2; -1)

\(x^2\) - 5\(x\) - 6 = 0

a = 1; b = -5; c = - 6

⇒ a - b + c = 1 - (-5) - 6 = 0

⇒ \(x_1\) = -1;    \(x_2\) = - \(\dfrac{c}{a}\) = - \(\dfrac{-6}{1}\) = 6

Vậy S = { -1;  6}

em khong biet

Gọi vận tốc ban đầu là \(x\) ( \(x\) > 0)

Sau hai giờ quãng đường người đó còn phải đi là: 160 - 2\(x\) (km)

Thời gian người đó đi nốt quãng đường còn lại là: \(\dfrac{160-2x}{x+8}\) (giờ)

Đổi 20 phút = \(\dfrac{20}{60}\) phút = \(\dfrac{1}{3}\) giờ 

Thời gian dự định ban đầu để đi hết quãng đường AB là: \(\dfrac{160}{x}\) ( giờ)

Theo bài ra ta có phương trình:

2  + \(\dfrac{1}{3}\)  + \(\dfrac{160-2x}{x+8}\)  = \(\dfrac{160}{x}\)

7\(x\)(\(x+8\)) + 3\(x\)( 160 - 2\(x\)) = 3.160.(\(x+8\))

7\(x^2\) + 56\(x\) + 480 \(x\) - 6\(x^2\)  = 480\(x\) + 3840

7\(x^2\) + 56\(x\) + 480\(x\) - 6\(x^2\) - 480\(x\) - 3840 =0

\(x^2\) + 56\(x\) - 3840 = 0 

Δ' = 28² + 3840 = 4624

\(x_1\) = \(\dfrac{-28+\sqrt{4624}}{1}\) = \(-28+68\) = 40 (thỏa mãn)

\(x_2\) = \(\dfrac{-28-\sqrt{4624}}{1}\) = -28 - 68 = -96  (loại)

Vậy \(x\) = 40

Kết luận vận tốc ban đầu của xe máy là: 40 km/h

  \(\left\{{}\begin{matrix}x-3y=5\\2x+3y=1\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}x-3y+2x+3y=5+1\\2x+3y=1\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}3x=6\\2x+3y=1\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}x=6:3\\2x+3y=1\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}x=2\\2x+3y=1\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}x=2\\2.2+3y=1\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}x=2\\3y=1-4\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}x=2\\3y=-3\end{matrix}\right.\)

⇒\(\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)

Vậy (\(x\);y) =(2; -1)

\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x+1}{x-1}\)   \(\left(\text{Đ}K:x\ge0;x\ne1\right)\)

    \(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}+1}{x-1}\right).\dfrac{x-1}{x+1}\) 

    \(=\dfrac{x+1}{x+1}=1\)

A =\(\sqrt{9}\) + \(\sqrt{16}\) + 2\(\sqrt{2}\) - \(\sqrt{8}\)

A = \(\sqrt{3^2}\) + \(\sqrt{4^2}\) + 2\(\sqrt{2}\) - 2\(\sqrt{2^3}\)

A = 3 + 4 + 2\(\sqrt{2}\) - 2\(\sqrt{2}\)

A = 7 + 0

A = 7

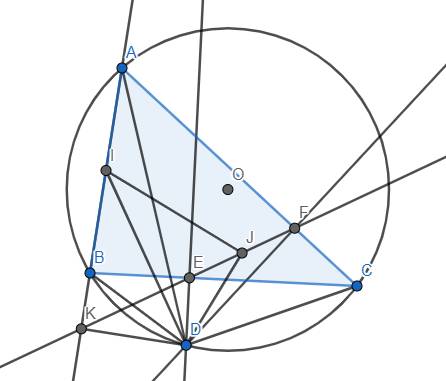
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.

b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp. 

Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)

\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)

c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm