Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vào năm 476, Romulus Augustus, Hoàng đế cuối cùng của Đế chế Tây La Mã, đã bị phế truất bởi Odoacer, "một kẻ man rợi" người Đức là vua nước Ý. Vào lúc ông phát động cuộc binh biến chống lại vị hoàng đế trẻ tuổi, Odoacer đang là thủ lĩnh của nhóm lính đánh thuê trong quân đội Đế Chế La Mã .Tại Piacenza, ông đã đánh bại tướng La Mã Orestes, người cha quyền lực của hoàng đế, và sau đó chiếm Ravenma, thủ đô của Đế chế Tây La Mã kể từ năm 402 . Dù người La Mã vẫn tiếp tực cai trị ở phía đông , việc Odoacer lên ngôi đã đánh dấu sự kết thúc của Đế chế La Mã nguyên thủy, với trung tâm ở Ý

"Cô ấy sẽ rời đi sáng mai" là một câu dùng thì tương lai đơn trong tiếng Anh. Bạn có thể dùng "will leave" hoặc "will be leaving" cũng được. Câu "leaves" không chính xác vì "leaves" là dạng hiện tại đơn của động từ "leave", không phù hợp trong trường hợp này.

a: \(1,25:\left(\dfrac{1}{2}-1\dfrac{1}{2}\right)-1,75\cdot\left(-20\%\right)\)
\(=\dfrac{5}{4}:\left(-1\right)-\dfrac{7}{4}\cdot\dfrac{-1}{5}\)
\(=-\dfrac{5}{4}+\dfrac{7}{20}=\dfrac{-25}{20}+\dfrac{7}{20}=-\dfrac{18}{20}=-\dfrac{9}{10}\)
b: \(\left(2,2+40\%\right):\left(\dfrac{1}{2}-1,25:20\%\right)\)
\(=\left(2,2+0,4\right):\left(0,5-1,25:0,2\right)\)
\(=2,6:\left(-5,75\right)=-\dfrac{52}{115}\)
c: \(\left[\dfrac{3}{4}-1,25:\left(-1\dfrac{1}{2}\right)\right]:\left(3,75-\dfrac{1}{2}:0,25\right)\)
\(=\left(\dfrac{3}{4}-\dfrac{5}{4}:\dfrac{-3}{2}\right):\left(\dfrac{15}{4}-\dfrac{1}{2}:\dfrac{1}{4}\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{5}{4}\cdot\dfrac{2}{3}\right):\left(\dfrac{15}{4}-2\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{5}{6}\right):\dfrac{7}{4}=\left(\dfrac{9}{12}+\dfrac{10}{12}\right):\dfrac{7}{4}\)
\(=\dfrac{19}{12}\cdot\dfrac{4}{7}=\dfrac{19}{21}\)
d: \(0,75\cdot\dfrac{-17}{13}-\dfrac{3}{4}\cdot\dfrac{-4}{13}-1,25\)
\(=0,75\cdot\dfrac{-17}{13}+\dfrac{3}{4}\cdot\dfrac{4}{13}-1,25\)
\(=0,75\cdot\left(-\dfrac{17}{13}+\dfrac{4}{13}\right)-1,25\)
=-0,75-1,25
=-2

a: \(2xy+x-y+xy^2+2xy\)
\(=x-y+xy^2+\left(2xy+2xy\right)\)
\(=x-y+xy^2+4xy\)
b: \(5xy^2+4y-4x\cdot2y^2\)
\(=4y+5xy^2-8xy^2\)
\(=4x-3xy^2\)
c: \(\sqrt{25}+\sqrt{36}+\sqrt{49}+...+\sqrt{100}\)
=5+6+7+8+9+10
=15+15+15
=45
d: Đặt \(A=1+4+9+16+...+9801+10000\)
Đặt \(B=1+8+27+...+729+1000\)
\(A=1+4+9+...+10000\)
\(=1^2+2^2+...+100^2\)
\(=\dfrac{100\left(100+1\right)\left(2\cdot100+1\right)}{6}\)
\(=\dfrac{100\cdot101\cdot201}{6}\)
\(B=1+8+27+...+1000\)
\(=1^3+2^3+...+10^3=\left(1+2+...+10\right)^2\)
\(=55^2\)
=>\(A-B=\dfrac{100\cdot101\cdot201}{6}-55^2=335325\)

b: \(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{100^2}< \dfrac{1}{99}-\dfrac{1}{100}\)
Do đó: \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
=>\(A< 1-\dfrac{1}{100}\)
=>A<1
=>0<A<1
=>A không là số tự nhiên
a: \(A=1+4+9+...+10000\)
\(=1^2+2^2+...+100^2\)
\(=\dfrac{100\left(100+1\right)\left(2\cdot100+1\right)}{6}\)
\(=\dfrac{100\cdot101\cdot201}{6}\)
\(B=1+8+27+...+1000\)
\(=1^3+2^3+...+10^3=\left(1+2+...+10\right)^2\)
\(=55^2\)
=>\(A-B=\dfrac{100\cdot101\cdot201}{6}-55^2=335325\)
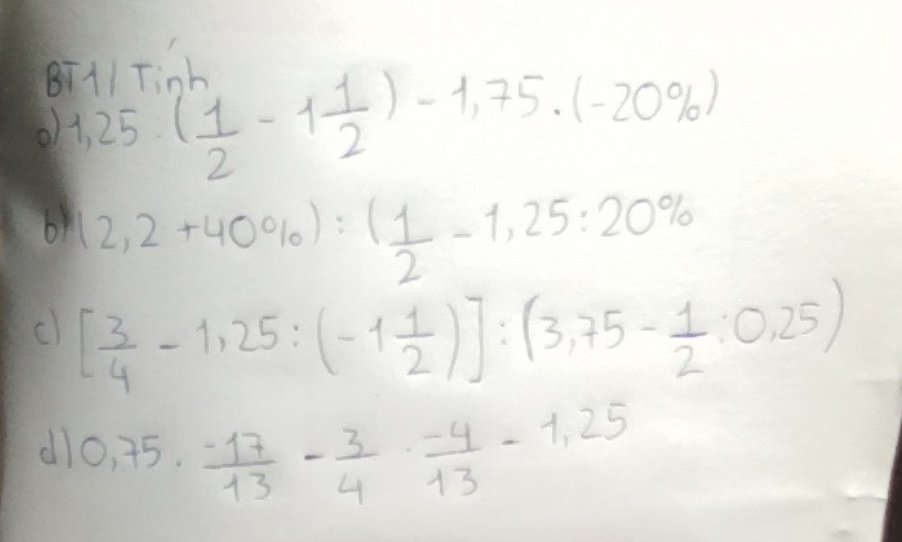
a; (\(\dfrac{3}{4}\))4.(\(\dfrac{8}{9}\))2
= (\(\dfrac{3}{2^2}\))4.(\(\dfrac{2^3}{3^2}\))2
= \(\dfrac{3^4}{2^8}\).\(\dfrac{2^6}{3^4}\)
= \(\dfrac{3^4.2^6}{3^4.2^6}\). \(\dfrac{1}{2^2}\)
= \(\dfrac{1}{2^2}\)
= \(\dfrac{1}{4}\)
b; (\(\dfrac{-3}{5}\))6.(-\(\dfrac{5}{3}\))5
= \(\dfrac{3^6}{5^6}\).\(\dfrac{\left(-5\right)^5}{3^5}\)
= \(\dfrac{-5^5.3^5}{5^5.3^5}\).\(\dfrac{3}{5}\)
= - 1.\(\dfrac{3}{5}\)
= - \(\dfrac{3}{5}\)