\(\overline{aaaa}:\overline{aa}+\overline{abab}:\overline{ab}\\ =\left(\overline{aa00}+\overline{aa}\right):\overline{aa}+\left(\overline{ab00}+\overline{ab}\right):\overline{ab}\\ =\left(\overline{aa}\times100+\overline{aa}\right):\overline{aa}+\left(\overline{ab}\times100+\overline{ab}\right):\overline{ab}\\ =\overline{aa}\times101:\overline{aa}+\overline{ab}\times101:\overline{ab}\\ =101+101=202\)

ab = ba x 3 + 6

a x 10 + b = ( b x 10 + a ) x 3 + 6

a x 10 + b = b x 30 + a x 3 + 6 

a x 10 - a x 3 = b x 30 - b + 6

a x 7 = b x 29 + 6

mk lm đc đến đây thuiiii

\(-\dfrac{1}{1\times4}-\dfrac{1}{4\times7}-\dfrac{1}{7\times10}-\dfrac{1}{10\times13}\)

\(=-\left(\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+\dfrac{1}{7\times10}+\dfrac{1}{10\times13}\right)\)

\(=-\dfrac{1}{3}\cdot\left(\dfrac{3}{1\times4}+\dfrac{3}{4\times7}+\dfrac{3}{7\times10}+\dfrac{3}{10\times13}\right)\)

\(=-\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}\right)\)

\(=-\dfrac{1}{3}\cdot\left(1-\dfrac{1}{13}\right)\)

\(=\dfrac{-1}{3}\cdot\dfrac{12}{13}\)

\(=\dfrac{-4}{13}\)

Thầy ơi thầy xem lại bài ạ 

a: \(B=\dfrac{4x+1}{2x+3}=\dfrac{4x+6-7}{2x+3}=2-\dfrac{7}{2x+3}\)

Để B min thì \(\dfrac{7}{2x+3}\) max

=>2x+3=1

=>2x=-2

=>x=-1

b: Để B max thì 2x+3=-1

=>2x=-4

=>x=-2

Ta có:

2024 ≡ 2024 (mod 2025)

2024² ≡ 1 (mod 2025)

2024³ ≡ 2024.2024² (mod 2025) ≡ 2024.1 (mod 2025) ≡ 2024 (mod 2025)

2024⁴ ≡ (2024²)² (mod 2025) ≡ 1² (mod 2025) ≡ 1 (mod 2025)

⇒ 2024 + 2024² + 2024³ + 2024⁴ ≡ 2024 + 1 + 2024 + 1 (mod 2025) 4050 ≡ (mod 2025) ≡ 0 (mod 2025)

Vậy (2024 + 2024² + 2024³ + 2024⁴) ⋮ 2025

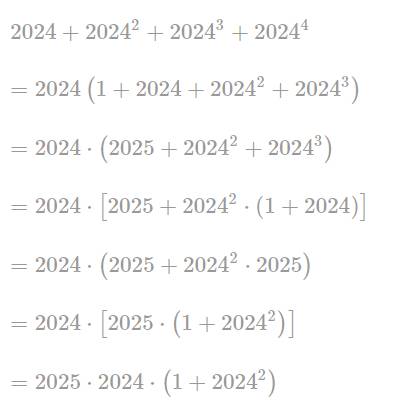
\(\Rightarrow2025\cdot2024\cdot\left(1+2024^2\right)\) ⋮ 2025 

\(\Rightarrow\left(2024+2024^2+2024^3+2024^4\right)⋮2025\)

= 2+2+2+2+2+... +2 (50 số hạng 2)
= 2.50 = 100
~hok tốt~
@3a3sontung

Ta có: \(\left\{{}\begin{matrix}x\left(x-3y\right)=4\left(y^2+2\right)\left(1\right)\\\left(xy-4\right)\left(x+y\right)=8\left(2\right)\end{matrix}\right.\)

\(\left(2\right)\Rightarrow xy-4;x+y\ne0\)

\(\left(1\right)\Leftrightarrow x^2-3xy-4y^2=8\) (*)

Từ (*) và (2) \(\Rightarrow x^2-3xy-4y^2=\left(xy-4\right)\left(x+y\right)\)

\(\Leftrightarrow x\left(x-4y\right)+y\left(x-4y\right)=\left(xy-4\right)\left(x+y\right)\)

\(\Leftrightarrow\left(x+y\right)\left(x-4y\right)=\left(x+y\right)\left(xy-4\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\left(L\right)\\x-4y=xy-4\end{matrix}\right.\) \(\Leftrightarrow x\left(1-y\right)+4\left(1-y\right)=0\)

\(\Leftrightarrow\left(x+4\right)\left(1-y\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\y=1\end{matrix}\right.\)

x = -4 thay vào (*), ta được: \(16-3.\left(-4\right)y-4y^2=8\)

\(\Leftrightarrow8+12y-4y^2=0\) \(\Leftrightarrow y^2-3y-2=0\) 

\(\Leftrightarrow y=\dfrac{3\pm\sqrt{17}}{2}\) ( dùng \(\Delta\) )

y=1 thay vào (*), ta được: \(x^2-3x-4=8\)

\(\Leftrightarrow x^2-3x-12=0\) \(\Leftrightarrow x=\dfrac{3\pm\sqrt{57}}{2}\)

Vậy ...

a: Xét tứ giác ABDC có

M là trung điểm chung của AD và BC

=>ABDC là hình bình hành

Hình bình hành ABDC có \(\widehat{BAC}=90^0\)

nên ABDC là hình chữ nhật

b: E đối xứng M qua AC

=>AC là đường trung trực của EM

=>AE=AM; CE=CM

ΔBAC vuông tại A

mà AM là đường trung tuyến

nên AM=CM=MB

AM=CM

AE=AM

CE=CM

Do đó: AM=MC=CE=AE

=>AMCE là hình thoi

c: AMCE là hình thoi

=>AE//CM

=>AE//BM

Xét tứ giác ABME có

AE//BM

AE=BM

Do đó: ABME là hình bình hành

=>AM cắt BE tại trung điểm của mỗi đường

mà I là trung điểm của AM

nên I là trung điểm của BE

=>B,I,E thẳng hàng