Tam bội (3n): 3n=36 NST

Tứ bội (4n): 4n=48 NST

Lục bội (6n): 6n=72 NST

Cửu bội (9n): 9n=108 NST

Thập nhị bội (12n): 12n= 144 NST

Tam nhiễm (2n+1): 2n+1= 25 NST

Một nhiễm (2n-1): 2n-1 = 23 NST

Câu 2.

Nhiệt lượng bếp tỏa ra trong thời gian \(t=3min=180s\) là:

\(Q=UIt=RI^2t=60\cdot2,5^2\cdot180=675000J\)

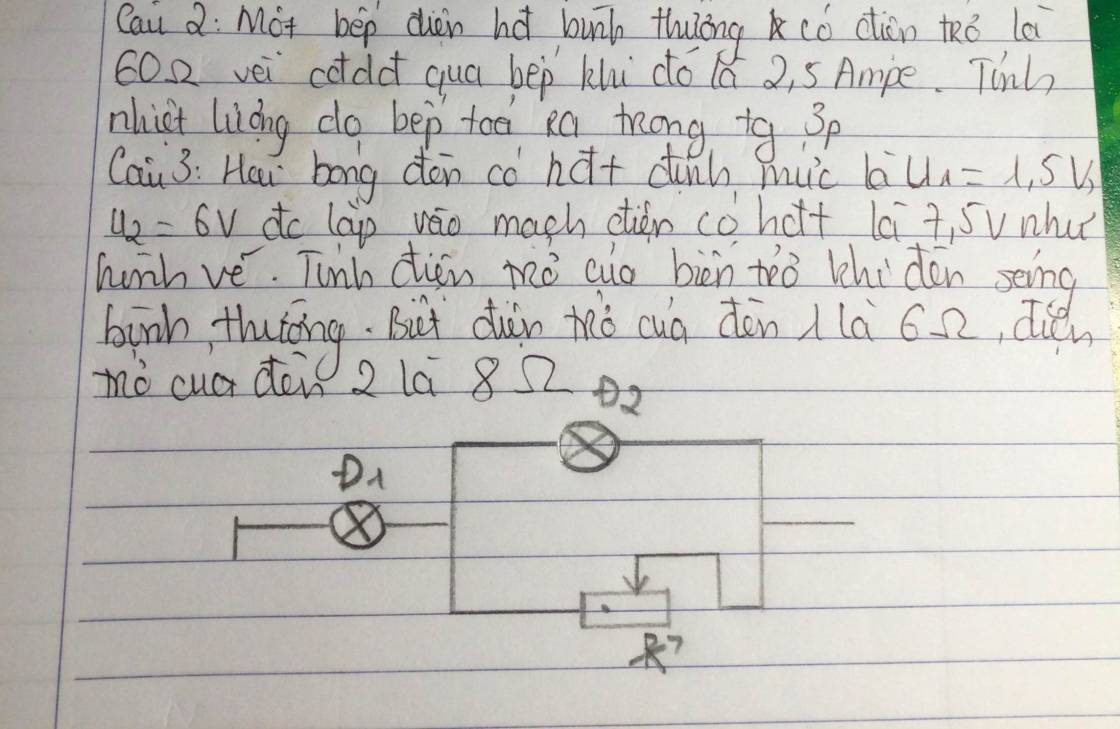
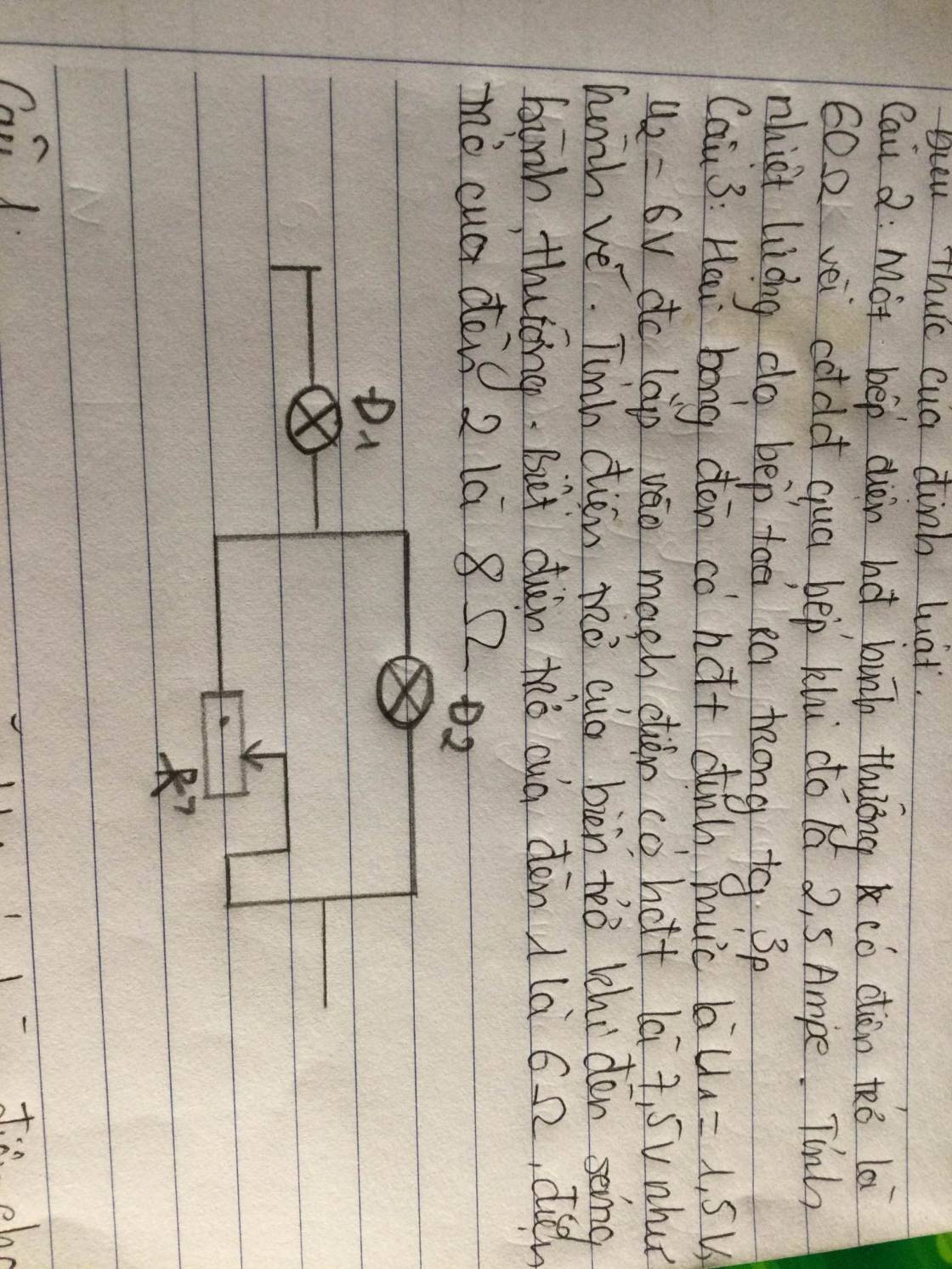
Câu 3.

\(I_{Đ1}=\dfrac{U_{Đ1}}{R_{Đ1}}=\dfrac{6}{6}=1A\)

\(I_{Đ2}=\dfrac{U_{Đ2}}{R_{Đ2}}=\dfrac{1,5}{8}=\dfrac{3}{16}A\)

\(I_b=I_{Đ1}-I_{Đ2}=1-\dfrac{3}{16}=\dfrac{13}{16}A\)

\(R_b=\dfrac{U_b}{I_b}=\dfrac{1,5}{\dfrac{13}{16}}=\dfrac{24}{13}\Omega\)

tóm tắt
R=60Ω

I=2,5 A

t = 3 phút = 180s 

                            Giải 

Nhiệt lượng do bếp tỏa ra  trong 3 phút là

Q= R.I².t = 60 . (2,5)² .180 =67500 J

beacause she studied hard , she got grade A for listening .

Because she studied hard, she got grade A for listening

a) có thể

b) Mạch BS : GGXXTAATGG

Bạn viết rõ đề bài ra nhé.

a/

Ta có

\(\widehat{BAC}=90^o\) (góc nt chắn nửa đường tròn)

\(\Rightarrow AB\perp AC\Rightarrow AE\perp AC;HF\perp AC\left(gt\right)\) => AE//HF

\(AC\perp AB\Rightarrow AF\perp AB;HE\perp AB\left(gt\right)\) => AF//HE

=> AEHF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

Mà \(\widehat{BAC}=90^o\left(cmt\right)\)

=> AEHF là hình CN

b/

Xét tg vuông EHA và tg vuông ABC có

\(\widehat{EAH}=\widehat{ACB}\) (cùng phụ với \(\widehat{ABC}\) )

=> tg EHA đồng dạng với tg ABC

\(\Rightarrow\dfrac{AE}{AC}=\dfrac{HE}{AB}\)

Mà AEHF là hình CN (cmt) => HE=AF (cạnh đối HCN)

\(\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\Rightarrow AE.AB=AF.AC\left(dpcm\right)\)

c/

\(\widehat{BAC}=90^o\left(cmt\right)\)

d/

Xét tg vuông HFC có

\(HI=CI\left(gt\right)\Rightarrow FI=HI=CI=\dfrac{HC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)

=> H; F; C cùng nằm trên đường tròn đường kính HC tâm I

=> đường tròn tâm I đường kính HC là đường tròn ngoại tiếp tg HFC

=> tg IHF cân tại I \(\Rightarrow\widehat{IFH}=\widehat{IHF}\)

Ta có

HF//AB (cùng vuông góc với AC) \(\Rightarrow\widehat{IHF}=\widehat{ABC}\) (góc đồng vị)

\(\Rightarrow\widehat{IFH}=\widehat{ABC}\) (1)

Xét tg vuông EAH và tg vuông HFE có

HE chung; AE=HF (cạnh đối hình CN) => tg EAH = tg HFE (Hai tg vuông có 2 cạnh góc vuông bàng nhau)

\(\Rightarrow\widehat{EAH}=\widehat{HFE}\)

Mà \(\widehat{EAH}=\widehat{ACB}\left(cmt\right)\)

\(\Rightarrow\widehat{HFE}=\widehat{ACB}\) (2)

Mà \(\widehat{ABC}+\widehat{ACB}=90^o\) (3)

Từ (1) (2) (3)

\(\Rightarrow\widehat{IFH}+\widehat{HFE}=\widehat{IFE}=\widehat{ABC}+\widehat{ACB}=90^o\)

=> EF là tiếp tuyến với (I)