0,75 = \(\dfrac{3}{4}\)

Theo sơ đồ ta có: Số lớn là: 0,75 : (4 - 3) x 4 = 3

                             Số bé là: 3 - 0,75 = 2,25 

Đs.... 

cô ơi làm thế nào để có được gp thế ạ?

con cu

đề sai sai :'))

giúp mình với nha mình đang vội

Số tiền giảm:

450000 × 20% = 90000 (đồng)

Giá mới là:

450000 - 90000 = 360000 (đồng)

Ta có

\(\dfrac{BM}{AM}=\dfrac{BC}{AC}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

\(\dfrac{CN}{AN}=\dfrac{BC}{AB}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

\(\Rightarrow\dfrac{BM}{AM}=\dfrac{CN}{AN}\Rightarrow\dfrac{BM}{CN}=\dfrac{AM}{AN}\) => MN//BC (Talet)

\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow\dfrac{AM}{b}=\dfrac{MN}{a}\)  (1)

Ta có

\(\dfrac{AM}{BM}=\dfrac{AC}{BC}=\dfrac{b}{a}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

\(\Rightarrow\dfrac{AM}{b}=\dfrac{BM}{a}=\dfrac{AM+BM}{a+b}=\dfrac{AB}{a+b}=\dfrac{b}{a+b}\)

\(\Rightarrow AM=\dfrac{b^2}{a+b}\) Thay vào (1)

\(\Rightarrow\dfrac{\dfrac{b^2}{a+b}}{b}=\dfrac{MN}{a}\Rightarrow\dfrac{b}{a+b}=\dfrac{MN}{a}\Rightarrow MN=\dfrac{ab}{a+b}\)

Ta có

����=����=��AMBM​=ACBC​=ba​ (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

����=����=��ANCN​=ABBC​=ba​ (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

⇒����=����⇒����=����⇒AMBM​=ANCN​⇒CNBM​=ANAM​ => MN//BC (Talet)

⇒����=����⇒���=���⇒ABAM​=BCMN​⇒bAM​=aMN​  (1)

Ta có

����=����=��BMAM​=BCAC​=ab​ (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)

⇒���=���=��+���+�=���+�=��+�⇒bAM​=aBM​=a+bAM+BM​=a+bAB​=a+bb​

⇒��=�2�+�⇒AM=a+bb2​ Thay vào (1)

⇒�2�+��=���⇒��+�=���⇒��=���+�⇒ba+bb2​​=aMN​⇒a+bb​=aMN​⇒MN=a+bab​
 

Diện tích khu vườn HCN theo đơn vị hm vuông là :

     5/2 × 4/5 = 2(km vuông) = 0,02(hm vuông)

          Đáp số : 0,02 hm vuông

Diện tích khu vườn:

\(\dfrac{5}{2}\times\dfrac{4}{5}=2\left(km^2\right)=200\left(hm^2\right)\)

bn sử dung nguyên tắc phá ngoặc là đc

4524-(864-999)-(36+999)

= 4524-864+999-36-999

= 4524+(999-999)-(864+36)

= 4524+0-900

= 3624

1 giờ = 3600 giây

1 ngày = 24 giờ \(\Rightarrow\) 1 ngày = 24 giờ x 3600 giây = 86400 giây.

cho tam giác ABC có AB=AC và M là trung điểm của BC

a. chứng minh tam giác AMB =  tam giác AMC

b.chứng minh AM vương góc BC

c.qua C kẻ đường thẳng d song song vs AB cắt tia AM tại N. chứng minhM là trung điểm của AN

\(\left(-\dfrac{3x}{5y^2}\right).\left(-\dfrac{5y^2}{6x^3}\right)\)

\(=\dfrac{-3x.\left(-5y^2\right)}{5y^2.6x^3}\)

\(=\dfrac{1}{2x^2}\)

29.(19 - 13) - 19.(19 - 13)

= 29.6 - 19.6

= 6.(29 - 19)

= 6.10

= 60

29 . (19 - 13 ) - 19 . ( 29 - 13 )

=29 . 6 - 19 . 16

=174 - 304

=130

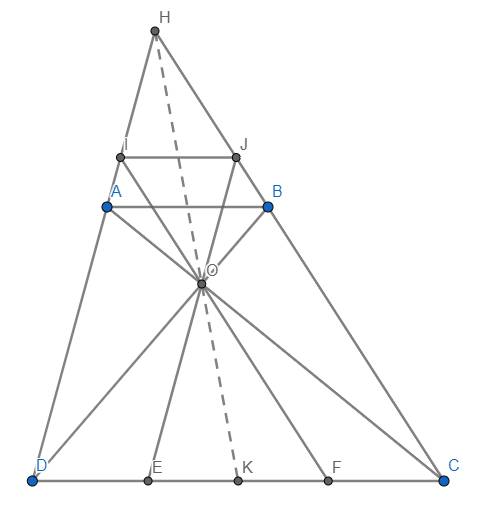
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)

Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)

c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)

Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\) 

Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB

d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)