
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để tính toán biểu thức này, chúng ta sẽ thực hiện các phép tính theo thứ tự ưu tiên từ trái qua phải. Hãy xem xét từng phần tử một: 1. 3/5: Chưa có phép tính nào trước nó, nên chúng ta giữ nguyên giá trị này. 2. 3/11 - (-3/7): Để trừ hai phân số, chúng ta cần tìm một số chung mẫu. Trong trường hợp này, số chung mẫu là 77. Chúng ta có thể viết lại phép tính này như sau: (3/11) + (3/7) * (11/11) = (3/11) + (33/77) = 36/77 3. (-2/97) - 1/35: Tương tự như trên, ta cần tìm số chung mẫu. Số chung mẫu trong trường hợp này là 3395. Chúng ta có thể viết lại phép tính như sau: (-2/97) * (35/35) - (1/35) * (97/97) = (-70/3395) - (97/3395) = -167/3395 4. (-23/44): Đây là một phân số đơn lẻ, chúng ta giữ nguyên giá trị này. Bây giờ, chúng ta có thể tính tổng của tất cả các phần tử: (3/5) + (36/77) - (167/3395) - (23/44) = (2566/3850) ≈ 0.667 Vậy kết quả của biểu thức là khoảng 0.667.
\(\dfrac{3}{5}+\dfrac{3}{11}-\left(-\dfrac{3}{7}\right)+\left(-\dfrac{2}{97}\right)-\dfrac{1}{35}-\dfrac{3}{4}+\left(-\dfrac{23}{44}\right)\)
\(=\left(\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{1}{35}\right)+\left(\dfrac{3}{11}-\dfrac{3}{4}-\dfrac{23}{44}\right)-\dfrac{2}{97}\)
\(=1-1-\dfrac{2}{97}=-\dfrac{2}{97}\)

Để chứng minh CMR này, chúng ta sẽ xem xét các trường hợp khác nhau khi n chia hết cho 4 và khi n không chia hết cho 4. Trường hợp 1: n chia hết cho 4 (n = 4k) Trong trường hợp này, chúng ta có n số a1, a2, a3, ..., an. Ta cần tính giá trị Sn = a1.a2 + a2.a3 + a3.a4 + ... + an.a1. Chú ý rằng mỗi số a1, a2, a3, ..., an xuất hiện đúng 2 lần trong Sn. Vì vậy, ta có thể viết lại Sn thành: Sn = (a1.a2 + a3.a4) + (a5.a6 + a7.a8) + ... + (an-1.an + a1.a2) Trong mỗi cặp số (ai.ai+1 + ai+2.ai+3), khi nhân hai số bằng nhau, ta luôn có kết quả là 1. Vì vậy, tổng của mỗi cặp số này sẽ luôn bằng 2. Vậy Sn = 2k = 0 khi và chỉ khi n chia hết cho 4. Trường hợp 2: n không chia hết cho 4 (n = 4k + m, với m = 1, 2, 3) Trong trường hợp này, chúng ta cũng có thể viết lại Sn thành: Sn = (a1.a2 + a3.a4) + (a5.a6 + a7.a8) + ... + (an-1.an + a1.a2) + an.a1 Nhưng lần này, chúng ta còn có thêm một số cuối cùng là an.a1. Xét mỗi cặp số (ai.ai+1 + ai+2.ai+3), khi nhân hai số bằng nhau, ta vẫn có kết quả là 1. Nhưng khi nhân số cuối cùng an.a1 với một số bằng -1, ta có kết quả là -1. Vì vậy, tổng của mỗi cặp số là 2, nhưng khi cộng thêm số cuối cùng an.a1, tổng sẽ có thể là 2 - 1 = 1 hoặc 2 + 1 = 3. Vậy Sn = 1 hoặc 3, không bao giờ bằng 0 khi n không chia hết cho 4. Từ hai trường hợp trên, ta có thể kết luận rằng Sn = 0 khi và chỉ khi n chia hết cho 4
Để chứng minh CMR này, chúng ta sẽ xét các trường hợp khác nhau khi n chia hết cho 4 và khi n không chia hết cho 4. Trường hợp 1: n chia hết cho 4 (n = 4k) Trong trường hợp này, chúng ta có n số a1, a2, a3, ..., an. Ta cần tính giá trị Sn = a1.a2 a2.a3 a3.a4 ... an.a1. Chú ý rằng mỗi số a1, a2, a3, ..., an xuất hiện đúng 2 lần trong Sn. Vì số bằng 1 hoặc -1, khi nhân hai số bằng nhau, ta luôn có kết quả là 1. Với n chia hết cho 4, ta có số lẻ các cặp số (ai.ai 1 ai 2.ai 3). Trong mỗi cặp này, khi nhân hai số bằng nhau, ta luôn có kết quả là 1. Vì vậy, tổng của mỗi cặp số này sẽ luôn bằng 1. Vậy Sn = 1 + 1 + ... + 1 (n/2 lần) = n/2 = 0 khi và chỉ khi n chia hết cho 4. Trường hợp 2: n không chia hết cho 4 (n = 4k + m, với m = 1, 2, 3) Trong trường hợp này, chúng ta cũng có số lẻ các cặp số (ai.ai 1 ai 2.ai 3). Trong mỗi cặp này, khi nhân hai số bằng nhau, ta luôn có kết quả là 1. Tuy nhiên, chúng ta còn có một số cuối cùng là an.a1. Với mỗi số bằng 1 hoặc -1, khi nhân với -1, ta sẽ đổi dấu của số đó. Vì vậy, tổng của mỗi cặp số là 1, nhưng khi cộng thêm số cuối cùng an.a1, tổng sẽ có thể là 1 - 1 = 0 hoặc 1 + 1 = 2. Vậy Sn = 0 hoặc 2, không bao giờ bằng 0 khi n không chia hết cho 4. Từ hai trường hợp trên, ta có thể kết luận rằng Sn = 0 khi và chỉ khi n chia hết cho 4.

Chứng minh rằng hai tia phân giác hai góc đối đỉnh không phải là hai tia đối nhau: Giả sử chúng ta có hai góc đối đỉnh AOB và COD, và hai tia phân giác của chúng là OA và OC. Để chứng minh rằng OA và OC không phải là hai tia đối nhau, chúng ta cần chứng minh rằng chúng không cùng nằm trên một đường thẳng. Giả sử rằng OA và OC cùng nằm trên một đường thẳng. Khi đó, ta có hai trường hợp để xét: Trường hợp 1: OA và OC không cắt nhau. Nếu OA và OC không cắt nhau, thì hai góc AOB và COD sẽ không có tia chung, điều này sẽ làm cho hai tia phân giác OA và OC không thể tồn tại. Trường hợp 2: OA và OC cắt nhau tại một điểm D. Nếu OA và OC cắt nhau tại một điểm D, thì tia OD sẽ là tia đối nhau của tia OA. Điều này đồng nghĩa với việc tia OD sẽ là tia phân giác của góc AOB. Tuy nhiên, điều này mâu thuẫn với giả thiết ban đầu vì chúng ta đã xác định rằng tia OA là tia phân giác của góc AOB. Vì vậy, hai tia OA và OC không thể cùng nằm trên một đường thẳng. Do đó, chúng ta có thể kết luận rằng hai tia phân giác của hai góc đối đỉnh không phải là hai tia đối nhau

\(4^5\cdot81^3\)
\(=\left(2^2\right)^5\cdot\left(3^4\right)^3\)
\(=2^{10}\cdot3^{12}\)
\(27^5\cdot8^3\)
\(=\left(3^3\right)^5\cdot\left(2^3\right)^3\)
\(=3^{15}\cdot2^8\)
này là phân số hay là gì vật bạn, bạn bấm vào kí hiệu \(\Sigma\) góc bên trái để có thể giúp các bạn trả lời đc câu hỏi mình nhé!
45x813=210x312
275x83=315x29

\(\left(\dfrac{9}{16}\right)^5\cdot x=\left(\dfrac{27}{64}\right)^3\)
\(\Leftrightarrow\left(\dfrac{3}{4}\right)^{10}\cdot x=\left(\dfrac{3}{4}\right)^9\)
\(\Rightarrow x=\left(\dfrac{3}{4}\right)^9:\left(\dfrac{3}{4}\right)^{10}\)
\(\Rightarrow x=\left(\dfrac{3}{4}\right)^{-1}\)
\(\Rightarrow x=\dfrac{4}{3}\)
Vậy x=4/3
(\(\dfrac{9}{16}\))5\(\times\) \(x\) = (\(\dfrac{27}{64}\))3
\(x\) = (\(\dfrac{27}{64}\))3 : (\(\dfrac{9}{16}\))5
\(x\) = (\(\dfrac{3^3}{2^6}\))3: (\(\dfrac{3^2}{2^4}\))5
\(x\) = \(\dfrac{3^9}{2^{18}}\) : \(\dfrac{3^{10}}{2^{20}}\)
\(x\) = \(\dfrac{3^9}{2^{18}}\) \(\times\) \(\dfrac{2^{20}}{3^{10}}\)
\(x\) = \(\dfrac{2^2}{3}\)
\(x\) = \(\dfrac{4}{3}\)

a) Xét ∆ ABK và ∆IBK có:
+\(\widehat{ABK}=\widehat{KBI}\)(gt)
+BK chung
+\(\widehat{BAK}=\widehat{BIK}\left(=90^o\right)\)
\(\Rightarrow\)∆ABK=∆IBK(ch-gnhon)
b) Ta có: \(\left\{{}\begin{matrix}KI\perp BC\left(gt\right)\\AD\perp BC\left(gt\right)\end{matrix}\right.\)
Do đó: KI//AD
\(\Rightarrow\widehat{DAI}=\widehat{AIK}\)(2 góc SLT) (1)
Ta có ∆ABK=∆IBK(cmt)
nên KA=KI (2 cạnh tương ứng)
Xét ∆KAI cân tại K
\(\Rightarrow\widehat{KAI}=\widehat{KIA}\)(2 góc đáy) (2)
Từ (1) và (2)\(\Rightarrow\widehat{DAI}=\widehat{KAI}\Leftrightarrow\widehat{DAI}=\widehat{IAC}\)
=> AI là tia pgiac(đpcm)

Bạn cần bài nào thì nên ghi chú rõ bài đó ra nhé. Nếu cần nhiều bài thì nên tách lẻ mỗi bài mỗi post để được hỗ trợ tốt hơn.

a, Góc so le trong với góc C là góc A2
Góc trong cùng phía với góc C là góc \(x\)AC
b, Góc so le trong với góc A1 là góc B1
Góc trong cùng phía với A1 là góc B2
Góc đồng vị với góc A1 là góc B3

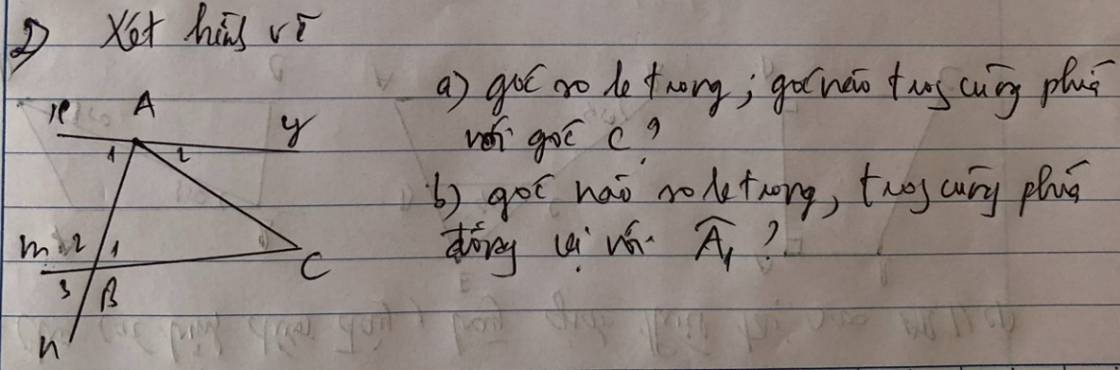
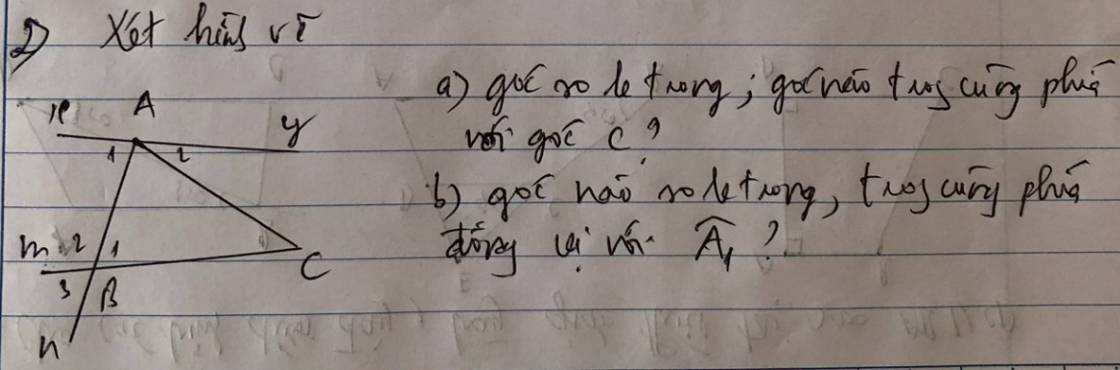
I = \(\dfrac{-\dfrac{4}{5}+\dfrac{4}{19}-\dfrac{4}{23}}{\dfrac{8}{5}-\dfrac{8}{19}+\dfrac{8}{23}}\)
I = \(\dfrac{-\left(\dfrac{4}{5}+\dfrac{4}{19}-\dfrac{4}{23}\right)}{2\left(\dfrac{4}{5}-\dfrac{4}{19}+\dfrac{4}{23}\right)}\)
I = - \(\dfrac{1}{2}\)