Biết x/125 < 24/36. Số tự nhiên lớn nhất có thể là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thời gian còn lại để Minh đi đến trường là:
7h-6h30p-10p=20p=1/3(giờ)
Vận tốc Minh cần đi là:
\(2,5:\dfrac{1}{3}=7,5\left(\dfrac{km}{h}\right)\)
Sau khi sửa xe thì đã là: \(6h30p+10p=6h40p\)
Vậy trong \(20p\) còn lại, Minh phải đi được \(2,5km\)
Mà \(20p=\dfrac{1}{3}\)h
Nên Minh phải đi với vận tốc: \(2,5.3=7,5\)\(km\)/h

Tuổi của mẹ hiện nay là:
5 × 7 = 35 ( tuổi )
Hiệu số tuổi của hai mẹ con là:
35 - 5 = 30 ( tuổi )
Ta có sơ đồ:
Mẹ : |----|----|----|----|
Con : |----|
Khi tuổi của mẹ gấp 4 lần tuổi con thì lúc đó con có số tuổi là:
30 : (4 - 1) × 1 = 10 ( tuổi)
Sau số năm nữa thì tuổi mẹ gấp 4 lần tuổi con là:
10 - 5 = 5 ( năm )
Đáp số: 5 năm

a: Diện tích xung quanh bể là:
\(\left(3+2\right)\cdot2\cdot1,6=5\cdot3,2=16\left(m^2\right)\)
b: Thể tích của bể nước là:
\(3\cdot2\cdot1,6=9,6\left(m^3\right)=9600\left(lít\right)\)

a: Vì ΔABC có BH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot BH\cdot AC\left(1\right)\)
Vì ΔABC có CK là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot CK\cdot AB\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot AC=CK\cdot AB\)
mà AC=AB
nên BH=CK
b: \(\dfrac{S_{BCD}}{S_{BCA}}=\dfrac{CD}{CA}\)
\(\dfrac{S_{CEB}}{S_{CBA}}=\dfrac{BE}{BA}\)
mà \(\dfrac{BE}{BA}=\dfrac{CD}{CA}\)
nên \(S_{BCD}=S_{BEC}\)

Bạn ghi phải có dấu thì mới hiểu chứ bạn ko ghi dấu thì khó hiểu lắm.
Sửa đề: Chiều cao là 3,5m
a: Diện tích xung quanh phòng là \(\left(6+4\right)\cdot2\cdot3,5=7\cdot10=70\left(m^2\right)\)
Diện tích trần là \(6\cdot4=24\left(m^2\right)\)
Diện tích cần quét vôi là:
\(70+24-10=84\left(m^2\right)\)
b: Số tiền cần trả là:
\(84\cdot45000=3780000\left(đồng\right)\)

2: Tổng thời gian đi là:
7h15p-6h48p=27p
Thời gian Hà đến cổng nhà Đoạt là \(\dfrac{27-3}{2}=12\left(phút\right)=0,2\left(giờ\right)\)
1: Số hộp kẹo trong 1 thùng là \(8\cdot4=32\left(hộp\right)\)
Tổng thể tích là \(32\cdot0,5=16\left(m^3\right)\)

A = \(\dfrac{1}{2}\) + \(\dfrac{5}{6}\) + \(\dfrac{11}{12}\) + \(\dfrac{19}{20}\) + ... + \(\dfrac{379}{380}\)
A = 1 - \(\dfrac{1}{2}\) + 1 - \(\dfrac{1}{6}\) + 1 - \(\dfrac{1}{12}\) + 1 - \(\dfrac{1}{20}\) +... + 1 - \(\dfrac{1}{380}\)
A = (1 + 1 + ... + 1) - (\(\dfrac{1}{2}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + ... + \(\dfrac{1}{380}\))
A = (1 + 1 + ... + 1) - (\(\dfrac{1}{1\times2}\) + \(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\)+ ... + \(\dfrac{1}{19\times20}\))
Xét dãy số: 1;2;3;4;;;;19 Dãy số này có 19 số hạng vậy
A = 1 x 19 - (\(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)+ \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + ... + \(\dfrac{1}{19}\) - \(\dfrac{1}{20}\))
A = 19 - (1 - \(\dfrac{1}{20}\))
A = 19 - \(\dfrac{19}{20}\)
A = \(\dfrac{361}{20}\) = \(\dfrac{a}{b}\)
Vậy a + b = 361 + 20 = 381
Lời giải:
$A=\frac{1}{2}+\frac{5}{6}+\frac{11}{12}+\frac{19}{20}+\frac{29}{30}+...+\frac{379}{380}$
$=(1-\frac{1}{2})+(1-\frac{1}{6})+(1-\frac{1}{12})+(1-\frac{1}{20})+....+(1-\frac{1}{380})$
$=19-(\frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}+...+\frac{1]{19\times 20})$
$=19-(\frac{2-1}{1\times 2}+\frac{3-2}{2\times 3}+\frac{4-3}{3\times 4}+...+\frac{20-19}{19\times 20})$
$=19-(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+..........+\frac{1}{19}-\frac{1}{20})$
$=19-(1-\frac{1}{20})=18+\frac{1}{20}=\frac{361}{20}$
$\Rightarrow a=361; b=20$
$\Rightarrow a+b=381$

Chiều cao của hình thang là:
765 x 2 : (56 + 29) = 18 (m)
Đáp số: 18 m

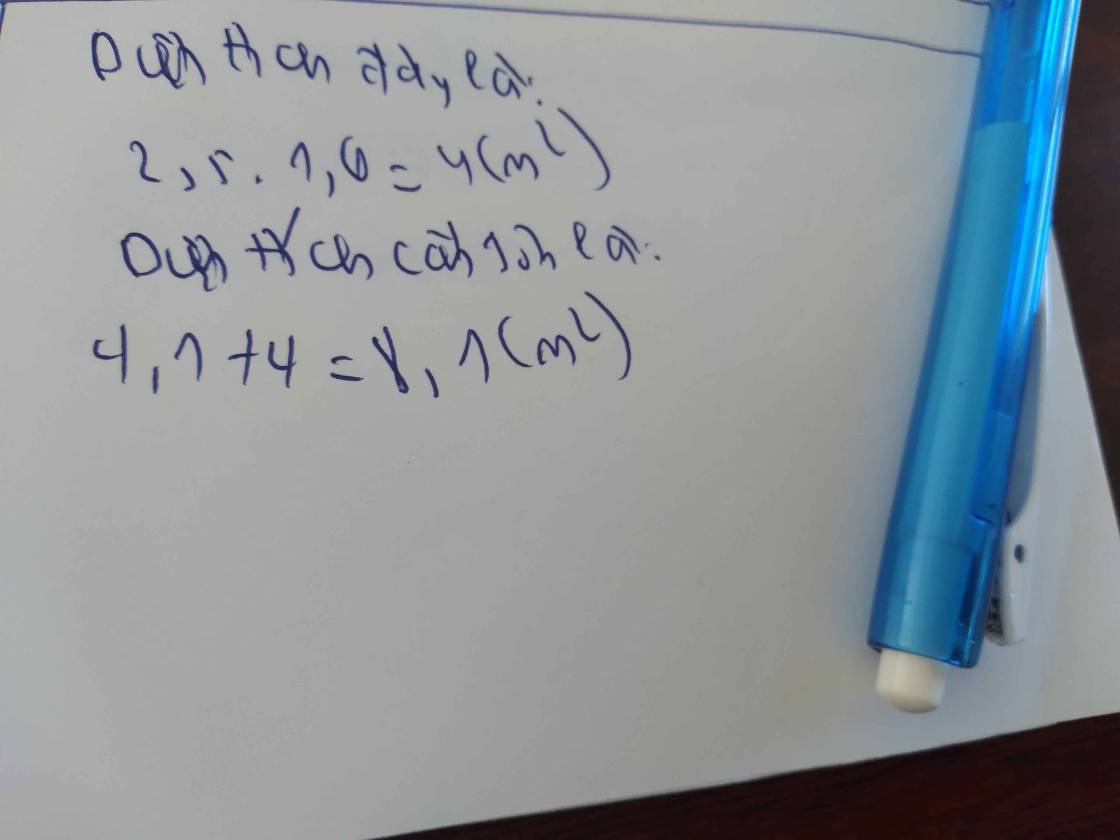

\(\dfrac{x}{125}< \dfrac{24}{36}\)
=>\(\dfrac{x}{125}< \dfrac{2}{3}\)
=>\(x< \dfrac{2}{3}\cdot125=\dfrac{250}{3}\)
=>số tự nhiên x lớn nhất là x=83
\(\dfrac{x}{125}\) < \(\dfrac{24}{36}\)
\(\dfrac{x}{125}\) < \(\dfrac{2}{3}\)
\(x\) < \(\dfrac{2}{3}\) x 125
\(x\) < \(\dfrac{250}{3}\)
\(x\) < 83\(\dfrac{1}{3}\)
Vậy số tự nhiên lớn nhất có thể của \(x\) là 83